浙江省宁波市2019届数学中考一模试卷（二）

更新时间：2024-11-06 浏览次数：633 类型：中考模拟

一、单选题

1. (2019·宁波模拟) 下列选项中的实数，属于无理数的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . ﹣9

答案解析收藏纠错 + 选题
2. (2019七下·永寿期末) 原子的一般直径是0.00000001cm，这个数据可以用科学记数法表示为（）

A . 1×10^﹣⁸ B . 1^﹣⁸ C . 1×10⁸ D . 1⁸

答案解析收藏纠错 + 选题
3. (2019·宁波模拟) 三通管的立体图如图所示，则这个几何体的左视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2019·宁波模拟) 下列计算正确的是（）

A . x³+x⁵＝x⁸ B . x³•x⁵＝x¹⁵ C . (x³)⁵＝x¹⁵ D . (2x⁵)³＝6x¹⁵

答案解析收藏纠错 + 选题
5. (2019·宁波模拟) 在一次中学生田径运动会上，参加男子跳高的20名运动员的成绩如表所示：

成绩(m)

1.55

1.60

1.65

1.70

1.75

1.80

人数

4

3

5

6

1

1

则这些运动员成绩的众数与中位数为（）

A . 1.55m，1.65m B . 1.65m，1，70m C . 1.70m，1.65m D . 1.80m，1.55m

答案解析收藏纠错 + 选题
6. (2019·宁波模拟) 如图，在4×4的正方形网格中，任选一个白色的小正方形并涂黑，使图中黑色部分的图形构成一个轴对称图形的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2019·宁波模拟) 已知点(﹣4，y₁)，(﹣2，y₂)，(1，y₃)都在直线y＝﹣ $\text{[math]}$ x+b上，则y₁ ， y₂ ， y₃的值的大小关系是（）

A . y₁＞y₂＞y₃ B . y₁＜y₂＜y₃ C . y₃＞y₁＞y₂ D . y₃＜y₁＜y₂

答案解析收藏纠错 + 选题
8. (2020九上·无锡月考) 如图，⊙O是正六边形ABCDEF的外接圆，P是弧EF上一点，则∠BPD的度数是（）

A . 30° B . 60° C . 55° D . 75°

答案解析收藏纠错 + 选题
9. (2019·宁波模拟) 某加工厂有工人50名，生产某种一个螺栓套两个螺母的配套产品，每人每天平均生产螺栓14个或螺母20个，应分配多少人生产螺栓，多少人生产螺母，能使生产出的螺栓和螺母刚好配套？设应安排x人生产螺栓，y人生产螺母，则所列方程组为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2019·宁波模拟) 如图，在Rt△ABC中，∠C＝90°，AC＝4，BC＝3，将△ABC绕AB上的点O顺时针旋转90°，得到△A′B′C′，连结BC′，若BC′∥A'B′，则OB的值为（）

A . $\text{[math]}$ B . 3 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2019·宁波模拟) 如图，平行四边形OABC的顶点O，B在y轴上，顶点A在反比例函数y＝﹣ $\text{[math]}$ 上，顶点C在反比例函数y＝ $\text{[math]}$ 上，则平行四边形OABC的面积是（）

A . 8 B . 10 C . 12 D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2019·宁波模拟) 勾股定理是人类最伟大的十个科学发现之一，西方国家称之为毕达哥拉斯定理，但远在毕达哥拉斯出生之前，这一定理早已被人们所利用，世界上各个文明古国都对勾股定理的发现和研究作出过贡献(希腊、中国、埃及、巴比伦、印度等)，特别是定理的证明，据说有400余种方法.其中在《几何原本》中有一种证明勾股定理的方法：如图所示，作CC⊥FH，垂足为G，交AB于点P，延长FA交DE于点S，然后将正方形ACED、正方形BCNM作等面积变形，得S_正方形_ACED＝S_▱_ACQS ， S_正方形_BCNM＝S_▱_BCQT ，这样就可以完成勾股定理的证明.对于该证明过程，下列结论错误的是（）

A . △ADS≌△ACB B . S_▱_ACQS＝S_矩形_APGF C . S_▱_CBTQ＝S_矩形_PBHG D . SE＝BC

答案解析收藏纠错 + 选题

二、填空题

13. (2019·宁波模拟) 因式分解：27a³﹣3a＝.

答案解析收藏纠错 + 选题
14. (2019·宁波模拟) 扇形的圆心角为60°，弧长为4πcm ，则此扇形的面积等于cm² ．

答案解析收藏纠错 + 选题
15. (2019·宁波模拟) 已知一组数据：1，4，x，2，6，9，若这组数据的众数为2，则这组数据的平均数为，中位数为.

答案解析收藏纠错 + 选题
16. (2019·宁波模拟) 关于x的方程 $\text{[math]}$ ＝3的解为.

答案解析收藏纠错 + 选题
17. (2019·宁波模拟) 当m，n是正实数，且满足mn＝m+2n时，就称点P(m， $\text{[math]}$ )为“新时代点”.如图，已知点A(0，10)与点M都在直线y＝﹣x+b上，点B，C是“新时代点”，且点B在线段AM上.若MC＝3，AM＝8 $\text{[math]}$ ，则△MBC的面积为.

答案解析收藏纠错 + 选题
18. (2019·宁波模拟) 某民房发生火灾.两幢大楼的部分截面及相关数据如图，小明在甲楼A处透过窗户E发现乙楼F处出现火灾，此时A，E，F在同一直线上.跑到一楼时，消防员正在进行喷水灭火，水流路线呈抛物线，在1.2m高的D处喷出，水流正好经过E，F.若点B和点E、点C和点F的离地高度分别相同，现消防员将水流抛物线向上平移5m，再向左后退m，恰好把水喷到F处进行灭火.

答案解析收藏纠错 + 选题

三、解答题

19. (2019·宁波模拟)
1. （1）计算：6sin60°+(π﹣ $\text{[math]}$ )⁰﹣ $\text{[math]}$ ﹣|﹣2|；
2. （2）化简：(2x﹣3y)²﹣(2x+y)(2x﹣y).
答案解析收藏纠错 + 选题
20. (2019·宁波模拟) 如图，在平行四边形ABCD中，点E，F分别是BC，AD的中点.
1. （1）求证：△ABE≌△CDF；
2. （2）若AE＝CE，BC＝2AB，BC＝6，求四边形AECF的面积.
答案解析收藏纠错 + 选题
21. (2019·宁波模拟) 宁波某中学有2500名学生，为了解全校每名学生的上学方式，该校数学兴趣小组在全校随机抽取了100名学生进行抽样调查.整理样本数据，得到扇形统计图如图：
1. （1）本次调查的个体是，样本容量是；
2. （2）扇形统计图中，乘私家车部分对应的圆心角是度；
3. （3）请估计该校2500名学生中，选择骑车和步行上学的一共有多少人？
答案解析收藏纠错 + 选题
22. (2022·鄞州模拟) 图①、图②、图③均是4×4的正方形网格，每个小正方形的顶点称为格点，每个小正方形的边长均为1.
1. （1）在图①、图②中，以格点为顶点，线段AB为一边，分别画一个平行四边形和菱形，并直接写出它们的面积.(要求两个四边形不全等)
2. （2）在图③中，以点A为顶点，另外三个顶点也在格点上，画一个面积最大的正方形，并直接写出它的面积.
答案解析收藏纠错 + 选题
23. (2019·宁波模拟) 如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，G是弧AC上的任意一点，AG，DC的延长线相交于点F.
1. （1）若CD＝8，BE＝2，求⊙O的半径；
2. （2）求证：∠FGC＝∠AGD；
3. （3）若直径AB＝10，tan∠BAC＝ $\text{[math]}$ ，弧AG＝弧BG，求DG的长.
答案解析收藏纠错 + 选题
24. (2019·宁波模拟) 城隍庙是宁波市的老牌商业中心，城隍庙商业步行街某商场购进一批品牌女装，购进时的单价是600元，根据市场调查，在一段时间内，销售单价是800元时，销售量是200件，销售单价每降低10元，就可多售出20件.
1. （1）求出销售量y(件)与销售单价x(元)之间的函数关系式；
2. （2）求出销售该品牌女装获得的利润W(元)与销售单价x(元)之间的函数关系式；
3. （3）若服装厂规定该品牌女装的销售单价不低于760元且不高于800元，则商场销售该品牌女装获得的最大利润是多少？
答案解析收藏纠错 + 选题
25. (2019·莲湖模拟) 在平面直角坐标系xOy中，抛物线y＝ax²+bx+c经过点A，B，C，已知A(﹣1，0)，B(5，0)，C(0，5)
1. （1）求抛物线与直线BC的表达式；
2. （2）如图1，P为线段BC上一点，过点P作y轴平行线，交抛物线于点D，当△BCD的面积最大时，求点P的坐标；
3. （3）如图2，抛物线顶点为E，EF⊥x轴于点F，N是线段EF上一动点，M(m，0)是x轴上一动点，若∠MNC＝90°，直接写出实数m的取值范围.
答案解析收藏纠错 + 选题
26. (2019·宁波模拟) 如图，矩形ABCD中，AD＝10，CD＝15，E是边CD上一点，且DE＝5，P是射线AD上一动点，过A，P，E三点的⊙O交直线AB于点F，连结PE，EF，PF，设AP＝x.
1. （1）当x＝5时，求AF的长.
2. （2）在点P的整个运动过程中.
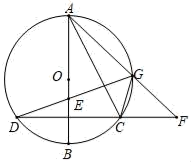
  ①tan∠PFE的值是否改变？若不变，求出它的值；若改变，求出它的变化范围；
  
  ②当矩形ABCD恰好有2个顶点落在⊙O上时，求x的值.
3. （3）若点A，H关于点O成中心对称，连结EH，CH.当△CEH是等腰三角形时，求出所有符合条件的x的值.(直接写出答案即可)
答案解析收藏纠错 + 选题