浙江省宁波市南三片2019届数学中考一模试卷

更新时间：2024-07-13 浏览次数：495 类型：中考模拟

一、单选题

1. (2019·新余模拟) $\text{[math]}$ 的倒数是（）

A . ﹣2019 B . $\text{[math]}$ C . $\text{[math]}$ D . 2019

答案解析收藏纠错 + 选题
2. (2019·宁波模拟) 宁波位于东南沿海，中国大陆海岸线中段，陆域总面积约为9816平方公里.其中9816用科学记数法表示为（）

A . 918.6×10 B . 91.86×10² C . 9.186×10³ D . 0.9186×10⁴

答案解析收藏纠错 + 选题
3. (2019·宁波模拟) 下列图形中是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2023七下·达州期中) 下列计算正确的是（）

A . （a³）²＝a⁵ B . a³⋅a⁵＝a⁸ C . a⁵+a²＝a⁷ D . a⁶÷a²＝a³

答案解析收藏纠错 + 选题
5. (2019·宁波模拟) 盒子里有3支红色笔芯，2支黑色笔芯，每支笔芯除颜色外均相同.从中任意拿出一支笔芯，则拿出黑色笔芯的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2019·宁波模拟) 由6个大小相同的小正方体拼成的几何体如图所示，则下列说法正确的是（）

A . 主视图的面积最大 B . 左视图的面积最大 C . 俯视图的面积最大 D . 三种视图的面积相等

答案解析收藏纠错 + 选题
7. (2019·宁波模拟) 今年3月12日，某学校开展植树活动，某植树小组20名同学的年龄情况如下表：

年龄（岁）

12

13

14

15

16

人数

1

4

3

5

7

则这20名同学年龄的众数和中位数分别是（）

A . 15，14 B . 15，15 C . 16，14 D . 16，15

答案解析收藏纠错 + 选题
8. (2019·路北模拟) 用半径为8的半圆围成一个圆锥的侧面，则圆锥的底面半径等于（）

A . 4 B . 6 C . 16π D . 8

答案解析收藏纠错 + 选题
9. (2019·宁波模拟) 一个三角形的两边长分别为3和6，第三边长是方程x²﹣10x+21＝0的解，则三角形的周长为（）

A . 12 B . 16 C . 12或16 D . 不能确定

答案解析收藏纠错 + 选题
10. (2019·宁波模拟) 如图，点A、B、C在⊙O上，若∠BAC=45°，OB=2，则图中阴影部分的面积为（）

A . π﹣2 B . $\text{[math]}$ C . π﹣4 D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2019·宁波模拟) 如图，在反比例函数y＝- $\text{[math]}$ 的图象上有一动点A，连结AO并延长交图象的另一支于点B，在第一象限内有一点C，满足AC＝BC，当点A运动时，点C始终在函数y＝ $\text{[math]}$ 的图象上运动，若tan∠CAB＝3，则k的值为（）

A . $\text{[math]}$ B . 6 C . 8 D . 18

答案解析收藏纠错 + 选题
12. (2019·宁波模拟) 如图，边长为正整数的正方形ABCD被分成了四个小长方形且点E，F，G，H在同一直线上（点F在线段EG上），点E，N，H，M在正方形ABCD的边上，长方形AEFM，GNCH的周长分别为6和10.则正方形ABCD的边长的最小值为（）

A . 3 B . 4 C . 5 D . 不能确定

答案解析收藏纠错 + 选题

二、填空题

13. (2019·株洲模拟) 比较大小：3 $\text{[math]}$ (填<，>或＝)．

答案解析收藏纠错 + 选题
14. (2024九下·郓城模拟) 二次根式 $\text{[math]}$ 在实数范围内有意义，x的取值范围是.

答案解析收藏纠错 + 选题
15. (2020·南昌模拟) 因式分解：4x²﹣y²＝.

答案解析收藏纠错 + 选题
16. (2019·宁波模拟) 不等式组 $\text{[math]}$ 的解集是.

答案解析收藏纠错 + 选题
17. (2019·宁波模拟) 如图，把一副三角板按如图放置，∠ACB＝∠ADB＝90°，∠CAB＝30°，∠DAB＝45°，点E是AB的中点，连结CE，DE，DC.若AB＝8，则△DEC的面积为.

答案解析收藏纠错 + 选题
18. (2019·宁波模拟) 如图，O是正方形ABCD边上一点，以O为圆心，OB为半径画圆与AD交于点E，过点E作⊙O的切线交CD于F，将△DEF沿EF对折，点D的对称点D'恰好落在⊙O上.若AB＝6，则OB的长为.

答案解析收藏纠错 + 选题

三、解答题

19. (2019·宁波模拟) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
20. (2019·宁波模拟) 某校开展“我最喜爱的一项体育活动”调查，要求每名学生必选且只能选一项，现随机抽查了m名学生，并将其结果绘制成不完整的条形统计图和扇形统计图.

结合以上信息解答下列问题：
1. （1） m＝.
2. （2）请补全上面的条形统计图；
3. （3）在图2中，乒乓球所对应扇形的圆心角＝；
4. （4）已知该校共有2100名学生，请你估计该校约有多少名学生最喜爱足球活动.
答案解析收藏纠错 + 选题
21. (2019·宁波模拟) 如图1是某商场从一楼到二楼的自动扶梯，图2是侧面示意图，MN是二楼楼顶，MN∥PQ，点C在MN上，且位于自动扶梯顶端B点的正上方，BC⊥MN.测得AB＝10米，在自动扶梯底端A处测得点C的仰角为50°，点B的仰角为30°，求二楼的层高BC（结果保留根号）
（参考数据：sin50°＝0.77，cos50°＝0.64，tan50°＝1.20）

答案解析收藏纠错 + 选题
22. (2024·犍为模拟) 如图，在△ABC中，∠C＝90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB于点E．
1. （1）求证：△ACD≌△AED；
2. （2）若∠B＝30°，CD＝1，求BD的长．
答案解析收藏纠错 + 选题
23. (2019·宁波模拟) 如图，在平面直角坐标系中，抛物线y=﹣x²+ax+b交x轴于A（1，0），B（3，0）两点，点P是抛物线上在第一象限内的一点，直线BP与y轴相交于点C.
1. （1）求抛物线y=﹣x²+ax+b的解析式；
2. （2）当点P是线段BC的中点时，求点P的坐标；
3. （3）在（2）的条件下，求sin∠OCB的值.
答案解析收藏纠错 + 选题
24. (2019·宁波模拟) 从宁海县到某市，可乘坐普通列车或高铁，已知高铁的行驶路程与普通列车的行驶路程之和是920千米，而普通列车的行驶路程是高铁的行驶路程的1.3倍.
1. （1）求普通列车的行驶路程；
2. （2）若高铁的平均速度（千米/时）是普通列车的平均速度（千米/时）的2.5倍，且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时，求高铁的平均速度.
答案解析收藏纠错 + 选题
25. (2019·宁波模拟) 定义：如图（1），E，F，G，H四点分别在四边形ABCD的四条边上，若四边形EFGH为菱形，我们称菱形EFGH为四边形ABCD的内接菱形.
1. （1）【动手操作】
  如图（2），网格中的每个小四边形都为正方形，每个小四边形的顶点叫做格点，由36个小正方形组成一个大正方形ABCD，点E、F在格点上，请在图（2）中画出四边形ABCD的内接菱形EFGH；
2. （2）【特例探索】
  如图（3），矩形ABCD，AB＝5，点E在线段AB上且EB＝2，四边形EFGH是矩形ABCD的内接菱形，求GC的长度；
3. （3）【拓展应用】
  如图（4），平行四边形ABCD，AB＝5，∠B＝60°，点E在线段AB上且EB＝2，
  
  ①请你在图（4）中画出平行四边形ABCD的内接菱形EFGH，点F在边BC上；
  
  ②在①的条件下，当BF的长最短时，BC的长为.
  
  （请同学们注意：以上作图题用直尺和圆规作图，不写作法，保留作图痕迹）
答案解析收藏纠错 + 选题
26. (2020·广州模拟) 如图1，在平面直角坐标系xOy中，半径为1的⊙O与x轴正半轴和y轴正半轴分别交于A，B两点，直线l：y＝kx+2（k＜0）与x轴和y轴分别交于P，M两点.
1. （1）当直线与⊙O相切时，求出点M的坐标和点P的坐标；
2. （2）如图2，当点P在线段OA上时，直线1与⊙O交于E，F两点（点E在点F的上方）过点F作FC∥x轴，与⊙O交于另一点C，连结EC交y轴于点D.
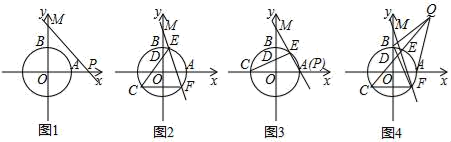
  ①如图3，若点P与点A重合时，求OD的长并写出解答过程；
  
  ②如图2，若点P与点A不重合时，OD的长是否发生变化，若不发生变化，请求出OD的长并写出解答过程；若发生变化，请说明理由.
3. （3）如图4，在（2）的基础上，连结BF，将线段BF绕点B逆时针旋转90°到BQ，若点Q在CE的延长线时，请用等式直接表示线段FC，FQ之间的数量关系.
答案解析收藏纠错 + 选题