
 B .
B .  C .
C . 


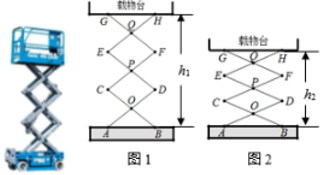




①请你通过分析求出此时y(元)与x(件)之间的函数关系式,并写出自变量x的取值范围;
②为使顾客一次性购买的数量越多,公司所获得的利润越大,公司应将最低销售单价调整为元?(其它销售条件不变)
如图1,等腰Rt△ABC的两个顶点B,C在直线MN上,点D是直线MN上一个动点(点D在点C的右边),BC=3,BD=m,在△ABC同侧作等腰Rt△ADE,∠ABC=∠ADE=90°,EF⊥MN于点F,连结CE.


①求DF的长;
②在判断AC⊥CE是否成立时,小明同学发现可以由以下两种思路解决此问题:
思路一:先证CF=EF,求出∠ECF=45°,从而证得结论成立.
思路二:先求DF,EF的长,再求CF的长,然后证AC2+CE2=AE2 , 从而证得结论成立.
请你任选一种思路,完整地书写本小题的证明过程.(如用两种方法作答,则以第一种方法评分)
将(1)中的两个等腰直角三角形都改为有一个角为的直角三角形,如图2,∠ABC=∠ADE=90°,∠BAC=∠DAE=30°,BC=3,BD=m,当4≤m≤6时,求CE长的范围.


第一步:沿三角形CAB的中位线ME将纸片剪成两部分,并在线段ME上任意取一点P,线段AB上任意取一点Q,沿PQ将四边形纸片MABE剪成两部分;
第二步:将PQ左侧纸片绕M点按顺时针方向旋转180°,使线段MA与MC重合,将PQ右侧纸片绕E点按逆时针方向旋转180°,使线段EC与EB重合,拼成一个与三角形纸片ABC面积相等的四边形纸片.(注:裁剪和拼图过程均无缝且不重叠)
求拼成的这个四边形纸片的周长的最小值与最大值的和.