浙江省绍兴市新昌县2019届数学中考一模试卷

更新时间：2019-09-29 浏览次数：505 类型：中考模拟

一、单选题

1. (2019·新昌模拟) ﹣8的相反数是（）

A . 8 B . ﹣8 C . $\text{[math]}$ D . ﹣ $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2019·新昌模拟) 据第六次人口普查数据显示，新昌常住人口约为380400人，数字380400用科学记数法可表示为（）

A . 3804×10² B . 0.3804×10⁶ C . 38.04×10⁴ D . 3.804×10⁵

答案解析收藏纠错 + 选题
3. (2019·新昌模拟) 由4个相同的立方体搭成的几何体如图所示.则它的主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2024九下·桃源期中) “绿水青山就是金山银山.”从这句话中随机选取一个汉字，选取“山”的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2019·新昌模拟) 下列各式计算正确的是（）

A . 5a²+a²＝5a⁴ B . (﹣3a)⁵＝﹣3a⁵ C . a¹²÷a⁴＝a³ D . ﹣a³•a²＝﹣a⁵

答案解析收藏纠错 + 选题
6. (2019·新昌模拟) 如图是用卡钳测量容器内径的示意图，现量得卡钳上A，D两个端点之间的距离为10cm， $\text{[math]}$ ，则容器的内径是（）

A . 5cm B . 10cm C . 15cm D . 20cm

答案解析收藏纠错 + 选题
7. (2019·新昌模拟) 将抛物线y＝3x²先向右平移1个单位长度，再向上平移4个单位长度，平移后抛物线的函数表达式是（）

A . y＝3(x+1)²+4 B . y＝3(x﹣1)²+4 C . y＝3(x+1)²﹣4 D . y＝3(x﹣1)²﹣4

答案解析收藏纠错 + 选题
8. (2024九下·绵阳模拟) 某校在配备现代化教学设备时，计划购买多媒体教学一体机和学生电脑共120台.已知多媒体教学一体机每8000元，学生电脑每台2500元，若购买这两种设备共花费52万元，求学校购买多媒体教学一体机和学生电脑各多少台？设购买多媒体教学一体机x台、学生电脑y台，根据题意列出的方程组正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2019·新昌模拟) 如图，在平面直角坐标系中，点B的坐标(0，2 $\text{[math]}$ )，∠AOC＝45°，∠ACO＝30°，则OC的长为（）

A . $\text{[math]}$ + $\text{[math]}$ B . $\text{[math]}$ ﹣ $\text{[math]}$ C . 2 $\text{[math]}$ + $\text{[math]}$ D . 2 $\text{[math]}$ + $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2019·新昌模拟) 我们将如图所示的两种排列形式的点的个数分别叫做“平行四边形数”和“正六边形数”.设第n个“平行四边形数”和“正六边形数”分别为a和b，若a+b＝103，则 $\text{[math]}$ 的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2023九下·杭州竞赛) 因式分解：x³﹣4x=．

答案解析收藏纠错 + 选题
12. (2023八下·枣阳期末) 已知函数y= $\text{[math]}$ ，则自变量x的取值范围是．

答案解析收藏纠错 + 选题
13. (2019·新昌模拟) 将二次函数y＝x²﹣8x+3化为y＝a(x﹣m)²+k的形式是.

答案解析收藏纠错 + 选题
14. (2019·新昌模拟) 如图，在矩形ABCD中，AB＝4，BC＝8，把△ABC沿着AC向上翻折得到△AEC，EC交AD边于点F，则点F到AC的距离是.

答案解析收藏纠错 + 选题
15. (2019·新昌模拟) 在平面直角坐标系中，反比例函数y＝ $\text{[math]}$ 的图象与经过原点O的直线1交于点A，B(n，﹣2)，过点A作AD⊥x轴，垂足为D，已知sin∠AOD＝ $\text{[math]}$ ，则k的值为.

答案解析收藏纠错 + 选题
16. (2019·新昌模拟) 已知菱形ABCD的边长为4，∠BAD＝60°，M是线段AD的中点，点P是对角线AC上的动点，连结PM，以P为圆心，PM长为半径作⊙P，当⊙P与菱形ABCD的边相切时，AP的长为.

答案解析收藏纠错 + 选题

三、解答题

17. (2019·新昌模拟)
1. （1）计算： $\text{[math]}$ +( $\text{[math]}$ ﹣π)⁰﹣4cos45°﹣|﹣3|；
2. （2）解分式方程： $\text{[math]}$ .
答案解析收藏纠错 + 选题
18. (2019·新昌模拟) 如图，正方形网格中有一段弧，弧上三点A，B，C均在格点上.
1. （1）请作图找出圆心P的位置(保留作图痕迹)，并写出它的坐标.
2. （2）求 $\text{[math]}$ 的长度.
答案解析收藏纠错 + 选题
19. (2019·新昌模拟) 新昌特色小吃是中华饮食文化宝库中的一块瑰宝，种类繁多，色香味美，著名的“米海茶”、“春饼”、“芋饺”、“炸面”、“炒年糕”等都是新昌特色小吃.一数学兴趣小组在全校范围内随机抽取了一些同学进行“我最喜爱的新昌特色小吃”的调查活动，将调查结果绘制成如下两幅不完整的统计图.请根据图中的信息，解答下列问题：
1. （1）请将条形统计图补充完整.
2. （2）在扇形统计图中，表示“炒年糕”对应的扇形的圆心角是多少度？
3. （3）若该校共有1200名学生，请你估计该校学生中最喜爱“米海茶”的学生有多少人？
答案解析收藏纠错 + 选题
20. (2019·新昌模拟) 游泳池应定期换水，打开排水孔排水时，池内的存水量Q(立方米)与排水时间t小时的函数关系如图所示.
1. （1）根据图象直接写出排水前游泳池的存水量，并计算出排水的速度.
2. （2）求Q关于t的函数表达式，并计算排水多久后，游泳池内还剩水156立方米.
答案解析收藏纠错 + 选题
21. (2019·新昌模拟) 如图，某轮船在点B处，测得小岛A在B的北偏东60°方向，然后向正东方向航行60海里到点C处，测得小岛A在C的北偏东30°方向.
1. （1）求小岛A到这艘轮船航行在点B时AB的长度.
2. （2）若轮船继续往正东方向行驶40海里到点D处，求AD的距离(精确到1海里).( $\text{[math]}$ ≈2.65)
答案解析收藏纠错 + 选题
22. (2019·新昌模拟) 某农场造一个矩形饲养场ABCD，如图所示，为节省材料，一边靠墙(墙足够长)，用总长为77m的木栏围成一块面积相等的矩形区域：矩形AEGH，矩形HGFD，矩形EBCF，并在①②③处各留1m装门(不用木栏)，设BE长为x(m)，矩形ABCD的面积为y(m²)
1. （1） ∵S_矩形_AEGH＝S_矩形_HGFD＝S_矩形_EBCF ， ∴S_矩形_AEFD＝2S_矩形_EBCF ， ∴AE：EB＝.
2. （2）求y关于x的函数表达式和自变量x的取值范围.
3. （3）当x为何值时，矩形ABCD的面积有最大值？最大值为多少？
答案解析收藏纠错 + 选题
23. (2019·新昌模拟) 在平面直角坐标系中，已知点A(0，4)，B(4，4)，点M，N是射线OC上两动点(OM＜ON)，且运动过程中始终保持∠MAN＝45°，小明用几何画板探究其中的线段关系.
1. （1）探究发现：当点M，N均在线段OB上时(如图1)，有OM²+BN²＝MN².
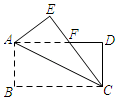
  他的证明思路如下：
  
  第一步：将△ANB绕点A顺时针旋转90°得△APO，连结PM，则有BN＝OP.
  
  第二步：证明△APM≌△ANM，得MP＝MM.
  
  第一步：证明∠POM＝90°，得OM²+OP²＝MP².
  
  最后得到OM²+BN²＝MN².
  
  请你完成第二步三角形全等的证明.
2. （2）继续探究：除(1)外的其他情况，OM²+BN²＝MN²的结论是否仍然成立？若成立，请证明；若不成立，请说明理由.
3. （3）新题编制：若点B是MN的中点，请你编制一个计算题(不标注新的字母)，并直接给出答案(根据编出的问题层次，给不同的得分).
答案解析收藏纠错 + 选题