浙江省台州市温岭市、天台县2019届数学中考一模试卷

更新时间：2019-09-25 浏览次数：397 类型：中考模拟

一、单选题

1. (2019·天台模拟) 下列四个几何体中，主视图是三角形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2020七上·承德期末) 中国人最先使用负数，魏晋时期的数学家刘徽在“正负术”的注文指出，可将算筹（小棍形状的记数工具）正放表示正数，斜放表示负数，如图，根据刘徽的这种表示法，观察图①，可推算图②中所得的数值为（）

A . ﹣1 B . ﹣2 C . ﹣3 D . ﹣4

答案解析收藏纠错 + 选题
3. (2019·天台模拟) 下列计算正确的是（）

A . a³+a⁴＝a⁷ B . a⁴•a⁵＝a⁹ C . 4^m•5^m＝9^m D . a³+a³＝2a⁶

答案解析收藏纠错 + 选题
4. (2024九下·昂仁模拟) 测试五位学生的“一分钟跳绳”成绩，得到五个各不相同的数据，在统计时出现了一处错误：将最高成绩写得更高了，则计算结果不受影响的是（）

A . 中位数 B . 平均数 C . 方差 D . 极差

答案解析收藏纠错 + 选题
5. (2019·天台模拟) 不等式4﹣2x≥0的解集在数轴上表示为（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2019·天台模拟) 将抛物线y＝x²﹣2x﹣3沿x轴折得到的新抛物线的解析式为（）

A . y＝﹣x²+2x+3 B . y＝﹣x²﹣2x﹣3 C . y＝x²+2x﹣3 D . y＝x²﹣2x+3

答案解析收藏纠错 + 选题
7. (2019·天台模拟) 如图，在△ABC中，点D是AB边上的一点，若∠ACD＝∠ B.AD＝1，AC＝2，△ADC的面积为S，则△BCD的面积为（）

A . S B . 2S C . 3S D . 4S

答案解析收藏纠错 + 选题
8. (2019·天台模拟) 如图，锐角△ABC中，BC＞AB＞AC，求作一点P，使得∠BPC与∠A互补，甲、乙两人作法分别如下：

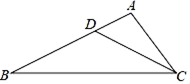
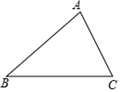
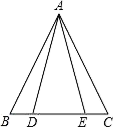
甲：以B为圆心，AB长为半径画弧交AC于P点，则P即为所求.

乙：作BC的垂直平分线和∠BAC的平分线，两线交于P点，则P即为所求.

对于甲、乙两人的作法，下列叙述正确的是（）

A . 两人皆正确 B . 甲正确，乙错误 C . 甲错误，乙正确 D . 两人皆错误

答案解析收藏纠错 + 选题

二、填空题

9. (2019·天台模拟) 如图，AB是⊙O的弦，半径OA＝5，sinA＝ $\text{[math]}$ ，则弦AB的长为.

答案解析收藏纠错 + 选题
10. (2019·天台模拟) 一项工程，先由甲独做，后乙加入合作直至完成，工程剩余工作量y与甲工作时间x（天）的函数关系如图所示，若要使工程提前4天完成，那么乙应该在甲工作第天后加入合作.

答案解析收藏纠错 + 选题
11. (2024九下·绍兴月考) 因式分解：a²﹣4= ．

答案解析收藏纠错 + 选题
12. (2019·天台模拟) 将一把直尺和一块含30°和60°角的三角板ABC按如图所示的位置放置，如果∠CDE＝40°，那么∠CAF的大小为.

答案解析收藏纠错 + 选题
13. (2019九上·湖州月考) 在一个不透明的盒子里有20个除颜色外均相同的小球，每次摸球前先将盒中的球摇匀，随机摸出一个球记下颜色后再放回盒中，通过大量重复实验后，发现摸到红球的频率稳定在0.4，由此估计盒子中红球的个数为.

答案解析收藏纠错 + 选题
14. (2019·天台模拟) 如图，先将边长为6m的正方形ABCD沿其对角线AC剪开，再把△ABC沿着AD方向平移，得到△AB′C′，当两个三角形重叠部分的面积为8cm²时，它移动的距离AA′等于cm.

答案解析收藏纠错 + 选题
15. (2019·天台模拟) 如图是反比例函数 $\text{[math]}$ 和 $\text{[math]}$ 在第一象限的图象，在 $\text{[math]}$ 上取点M，分别作两坐标轴的垂线交 $\text{[math]}$ 于点A、B，连按OA、OB，则图中阴影部分面积为.

答案解析收藏纠错 + 选题
16. (2019九上·台州期中) 在矩形ABCD中，AB＝3，BC＝4，点E、F分别在BC与CD上，且∠EAF＝45°.如图甲，若EA＝EF，则EF＝；如图乙，若CE＝CF，则EF＝.

答案解析收藏纠错 + 选题

三、解答题

17. (2019·天台模拟)
1. （1）计算： $\text{[math]}$ ；
2. （2）化简：﹣2（a﹣3）+（a+1）²
答案解析收藏纠错 + 选题
18. (2019八上·陇西期中) 如图，已知D、E两点在线段BC上，AB＝AC，AD＝AE．证明：BD＝CE．

答案解析收藏纠错 + 选题
19. (2019·天台模拟) 某地下车库出口处安装了“两段式栏杆”，如图1所示，点A是栏杆转动的支点，点E是栏杆；两段的联结点.当车辆经过时，栏杆AEF最多只能升起到如图2所示的位置，其示意图如图3所示（栏杆宽度忽略不计，EF长度远大于车辆宽度），其中AB⊥BC，EF∥BC，∠AEF＝143°，AB＝AE＝1.2米，该地下车库出口的车辆限高标志牌设置如图4是否合理？请通过计算说明理由.（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）

答案解析收藏纠错 + 选题
20. (2019·天台模拟) 如图，在Rt△ABC中，∠C＝90°，BD平分∠ABC，点O在AB上，以点O为圆心，OB为半径的圆经过点D，交BC于点E
1. （1）求证：AC是⊙O的切线；
2. （2）若OB＝2，CD＝ $\text{[math]}$ ，求图中阴影部分的面积（结果保留 $\text{[math]}$ ）.
答案解析收藏纠错 + 选题

21. (2019·天台模拟) 从共享单车，共享汽车等共享出行到共享雨伞等共享物品，各式各样的共享经济模式在各个领域迅速的普及，根据国家信息中心发布的中国分享经济发展报告2017显示，参与共享经济活动超6亿人，比上一年增加约1亿人.

（1）为获得北京市市民参与共享经济活动信息，下列调查方式中比较合理的是；

A . 对某学校的全体同学进行问卷调查 B . 对某小区的住户进行问卷调查 C . 在全市里的不同区县，选取部分市民进行问卷调查

（2）调查小组随机调查了延庆区市民骑共享单车情况，某社区年龄在12～36岁的人有1000人，从中随机抽取了100人，统计了他们骑共享单车的人数，并绘制了如下不完整的统计图表.如图所示.骑共享单车的人数统计表

年龄段（岁）	频数	频率
12≤x＜16	2	0.02
16≤x＜20	3	0.03
20≤x＜24	15	a
24≤x＜28	25	0.25
28≤x＜32	b	0.30
32≤x＜36	25	0.25

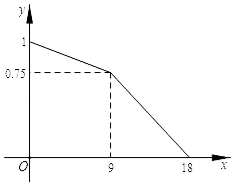
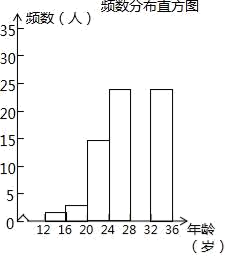
根据以上信息解答下列问题：

①统计表中的a＝；b＝；

②补全频数分布直方图；

③试估计这个社区年龄在20岁到32岁（含20岁，不含32岁）骑共享单车的人有多少人？

答案解析收藏纠错 + 选题

22. (2019·天台模拟) 某水果店计划购进甲、乙两种新出产的水果共140千克，这两种水果的进价、售价如表所示：

进价（元/千克）

售价（元/千克）

甲种

5

8

乙种

9

13
1. （1）若该水果店预计进货款为1000元，则这两种水果各购进多少千克？
2. （2）若该水果店决定乙种水果的进货量不超过甲种水果的进货量的3倍，应怎样安排进货才能使水果店在销售完这批水果时获利最多？此时利润为多少元？
答案解析收藏纠错 + 选题
23. (2019·天台模拟) 如图1，AB是曲线，BC是线段，点P从点A出发以不变的速度沿A﹣B﹣C运动，到终点C停止，过点P分别作x轴、y轴的垂线分别交x轴、y轴于点M、点N，设矩形MONP的面积为S运动时间为（秒），S与t的函数关系如图2所示，（FD为平行x轴的线段）
1. （1）直接写出k、a的值.
2. （2）求曲线AB的长l.
3. （3）求当2≤t≤5时关于的函数解析式.
答案解析收藏纠错 + 选题
24. (2019·天台模拟) 如图1，平面内有一点P到△ABC的三个顶点的距离分别为PA、PB、PC，若有PA²＝PB²+PC²则称点P为△ABC关于点A的勾股点.
1. （1）如图2，在4×5的网格中，每个小正方形的长均为1，点A、B、C、D、E、F、G均在小正方形的顶点上，则点D是△ABC关于点的勾股点；在点E、F、G三点中只有点是△ABC关于点A的勾股点.
2. （2）如图3，E是矩形ABCD内一点，且点C是△ABE关于点A的勾股点，
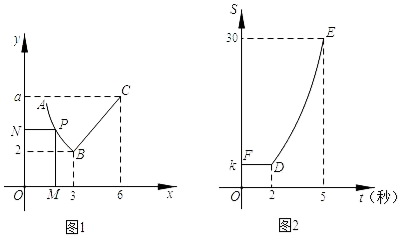
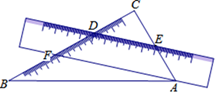
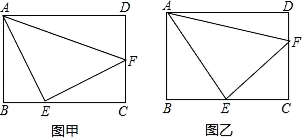
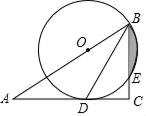
  ①求证：CE＝CD；
  
  ②若DA＝DE，∠AEC＝120°，求∠ADE的度数.
3. （3）矩形ABCD中，AB＝5，BC＝6，E是矩形ABCD内一点，且点C是△ABE关于点A的勾股点，
  ①若△ADE是等腰三角形，求AE的长；
  
  ②直接写出AE+ $\text{[math]}$ BE的最小值.
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

浙江省台州市温岭市、天台县2019届数学中考一模试卷

副标题：

*注意事项：

浙江省台州市温岭市、天台县2019届数学中考一模试卷

试题分析

总体分析

题量分析

难度分析

知识点分析

	进价（元/千克）	售价（元/千克）
甲种	5	8
乙种	9	13