浙江省温州市鹿城区2019届数学中考模拟试卷（3月)

更新时间：2024-07-13 浏览次数：386 类型：中考模拟

一、单选题

1. (2020八上·张店期末) 在0.3，﹣3，0，﹣ $\text{[math]}$ 这四个数中，最大的是（）

A . 0.3 B . ﹣3 C . 0 D . ﹣ $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2019·鹿城模拟) 在开展“爱心捐助某灾区”的活动中，某团支部8名团员捐款的数额（单位：元）分别为3，5，6，5，5，6，5，10，这组数据的中位数是（）

A . 3元 B . 5元 C . 6元 D . 10元

答案解析收藏纠错 + 选题
3. (2019·鹿城模拟) 一个几何体的三视图如图所示，这个几何体是（）

A . 球 B . 圆柱 C . 圆锥 D . 立方体

答案解析收藏纠错 + 选题
4. (2019·鹿城模拟) 下列计算正确的是（　　）

A . a²+a²=a⁴ B . 2a²×a³=2 C . （a²）³=a⁶ D . 3a﹣2a=1

答案解析收藏纠错 + 选题
5. (2019·鹿城模拟) 如图，在△ABC中，∠C＝90°，AB＝10，BC＝6，则sin∠A＝（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022九下·金华月考) 下列选项中，可以用来证明命题“若a²＞b² ，则a＞b“是假命题的反例是（）

A . a＝﹣2，b＝1 B . a＝3，b＝﹣2 C . a＝0，b＝1 D . a＝2，b＝1

答案解析收藏纠错 + 选题
7. (2019·鹿城模拟) 甲，乙工程队分别承接600米，800米的道路修建工程，已知乙比甲每天多修建12米，结果甲比乙提早1天完成，问甲每天修建多少米？设甲每天修建x米，根据题意可列出方程是（）

A . $\text{[math]}$ ＝ $\text{[math]}$ ﹣1 B . $\text{[math]}$ ＝ $\text{[math]}$ +1 C . $\text{[math]}$ ＝ $\text{[math]}$ ﹣1 D . $\text{[math]}$ ＝ $\text{[math]}$ +1

答案解析收藏纠错 + 选题
8. (2019·鹿城模拟) 对于代数式ax²﹣2bx﹣c，当x取﹣1时，代数式的值为2，当x取0时，代数式的值为1，当x取3时，代数式的值为2，则当x取2时，代数式的值是（）

A . 1 B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题
9. (2019·鹿城模拟) 如图，已知抛物线y＝x²﹣2x﹣3与x轴相交于点A，B，若在抛物线上有且只有三个不同的点C₁ ， C₂ ， C₃ ，使得△ABC₁ ， △ABC₂ ， △ABC₃的面积都等于a，则a的值是（）

A . 6 B . 8 C . 12 D . 16

答案解析收藏纠错 + 选题
10. (2019·鹿城模拟) 如图，AB，BC是⊙O的弦，∠B=60°，点O在∠B内，点D为 $\text{[math]}$ 上的动点，点M，N，P分别是AD，DC，CB的中点.若⊙O的半径为2，则PN+MN的长度的最大值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2019·鹿城模拟) 因式分解：x²﹣2x=．

答案解析收藏纠错 + 选题
12. (2018八上·黄陂月考) 如图，∠ACD是△ABC的外角，若∠B＝50°，∠ACD＝120°，则∠A＝.

答案解析收藏纠错 + 选题
13. (2019·鹿城模拟) 某市号召居民节约用水，为了解居民用水情况，随机抽查了20户家庭某月的用水量，结果如下表：

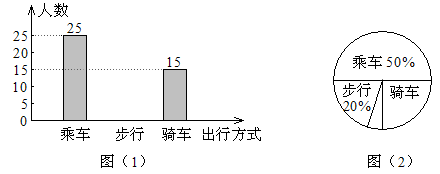
户数

8

6

6

用水量（吨）

4

6

7

则这20户家庭的该月平均用水量为吨.

答案解析收藏纠错 + 选题
14. (2019·鹿城模拟) 已知扇形的圆心角为120°，弧长为4π，则扇形的面积是.

答案解析收藏纠错 + 选题
15. (2019·鹿城模拟) 如图，点A是反比例函数y= $\text{[math]}$ 图象上的任意一点，过点A作AB∥x轴，AC∥y轴，分别交反比例函数y= $\text{[math]}$ 的图象于点B，C，连接BC，E是BC上一点，连接并延长AE交y轴于点D，连接CD，则S_△_DEC﹣S_△_BEA=.

答案解析收藏纠错 + 选题
16. (2019·鹿城模拟) 如图，四边形ABCD是矩形，AD＝5，AB＝ $\text{[math]}$ ，点E在CD边上，DE＝2，连接BE，F是BE边上的一点，过点F作FG⊥AB于G，连接DG，将△ADG沿DG翻折的△PDG，设EF＝x，当P落在△EBC内部时（包括边界），x的取值范围是.

答案解析收藏纠错 + 选题

三、解答题

17. (2019·鹿城模拟)
1. （1）计算： $\text{[math]}$ +（ $\text{[math]}$ ）^﹣¹﹣|﹣3|
2. （2）先化简，再求值：（a﹣2）（a+2）﹣a（a﹣1），其中a＝﹣1
答案解析收藏纠错 + 选题
18. (2020八下·兴宾期中) 如图，在Rt△ABC中，∠BAC＝90°，AD平分∠BAC，过AC的中点E作FG∥AD，交BA的延长线于点F，交BC于点G，
1. （1）求证：AE＝AF；
2. （2）若BC＝ $\text{[math]}$ AB，AF＝3，求BC的长.
答案解析收藏纠错 + 选题
19. (2019·秦安模拟) 学了统计知识后，小红就本班同学上学“喜欢的出行方式”进行了一次调查，图（1）和图（2）是她根据采集的数据绘制的两幅不完整的统计图，请根据图中提供的信息解答以下问题：
1. （1）补全条形统计图，并计算出“骑车”部分所对应的圆心角的度数.
2. （2）若由3名“喜欢乘车”的学生，1名“喜欢骑车”的学生组队参加一项活动，现欲从中选出2人担任组长（不分正副），求出2人都是“喜欢乘车”的学生的概率，（要求列表或画树状图）
答案解析收藏纠错 + 选题
20. (2019·鹿城模拟) 在直角坐标系中，我们把横，纵坐标都是整数的点称为整点，记顶点都是整点的三角形为整点三角形.如图，已知整点A（2，4），B（1，1），请在所给网格区域（含边界）上按要求画整点三角形.

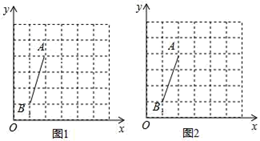
①在图1中画一个Rt△PAB，使点P落在坐标轴上；

②在图2中画一个等腰△PAB，使得△PAB的面积为4.

答案解析收藏纠错 + 选题
21. (2024八下·丰城月考) 如图，▱ABCD与抛物线y＝﹣x²+bx+c相交于点A，B，D，点C在抛物线的对称轴上，已知点B（﹣1，0），BC＝4.
1. （1）求抛物线的解析式；
2. （2）求BD的函数表达式.
答案解析收藏纠错 + 选题
22. (2019·鹿城模拟) 如图，在⊙O中，半径OD⊥直径AB，CD与⊙O相切于点D，连接AC交⊙O于点E，交OD于点G，连接CB并延长交⊙于点F，连接AD，EF.
1. （1）求证：∠ACD＝∠F；
2. （2）若tan∠F＝ $\text{[math]}$
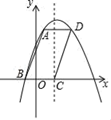
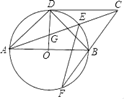
  ①求证：四边形ABCD是平行四边形；
  
  ②连接DE，当⊙O的半径为3时，求DE的长.
答案解析收藏纠错 + 选题
23. (2019·鹿城模拟) 小王准备给家中长为3米的正方形ABCD电视墙铺设大理石，按图中所示的方案分成9块区域分别铺设甲，乙，丙三种大理石（正方形EFGH是由四块全等的直角三角形围成），
1. （1）已知甲大理石的单价为150元/m² ，乙大理石的单价为200元/m² ，丙大理石的单价为300元/m² ，整个电视墙大理石总价为1700元.
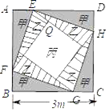
  ①当铺设甲，乙大理石区域面积相等时，求铺设丙大理石区域的面积.
  
  ②设铺设甲，乙大理石区域面积分别为xm² ， ym² ，当丙的面积不低于1m²时，求出y关于x的函数关系式，并写出y的最大值.
2. （2）若要求AE：AF＝1：2，EQ：FQ＝1：3，甲，乙大理石单价之和为300元/m² ，丙大理石的单价不低于300元/m² ，铺设三种大理石总价为1620元，求甲的单价取值范围.
答案解析收藏纠错 + 选题
24. (2019·鹿城模拟) 如图在矩形ABCD中，AB＝8，过对角线AC的中点O作直线PE，交AB于点P，交CD于点Q，交射线AD于点E，连接CE，作点Q关于CE对称的对称点Q′，以Q′为圆心，为CQ′半径作⊙Q′，交CE于点M，设BC＝x.
1. （1）请说明△AOP≌△COQ的理由.
2. （2）若AP＝5，
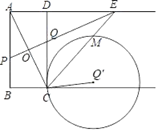
  ①请用x的代数式表示DE的长.
  
  ②当△DQM为直角三角形时，请求出所有满足条件的BC的值.
3. （3）若存在⊙Q′同时与直线AC和直线AD相切，请直接写出⊙Q′的半径.
答案解析收藏纠错 + 选题