江苏省东台市第七联盟2019届九年级上学期数学12月月考试卷

更新时间：2019-10-15 浏览次数：279 类型：月考试卷

一、单选题

1. (2021九上·绵阳月考) 抛物线y=2(x-3)²-1的顶点坐标是（）

A . （3，1） B . （3，-1） C . （-3，1） D . （-3，-1）

答案解析收藏纠错 + 选题
2. (2018九上·东台月考) Rt△ABC中，∠C=90°，a=4，b=3，则cosA的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2018九上·东台月考) 如图，已知a∥b∥c，直线m分别交直线a、b、c于点A、B、C，直线n分别交直线a、b、c于点D、E、F，若 $\text{[math]}$ = $\text{[math]}$ ，则 $\text{[math]}$ 的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 1

答案解析收藏纠错 + 选题
4. (2018九上·东台月考) 如图，若A，B，C，P，Q，甲、乙、丙、丁都是方格纸中的格点，为使△ABC∽△PQR，则点R应是甲、乙、丙、丁四点中的（）

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题
5. (2018九上·东台月考) 如图，在□ABCD中，点E是边AD的中点，EC交对角线BD于点F，则DF：FB等于（）

A . 1∶1 B . 1∶2 C . 1∶3 D . 2∶3

答案解析收藏纠错 + 选题
6. (2018九上·东台月考) 在同一时刻太阳光线是平行的，如果高1.5米的测杆影长3米，那么此时影长36米的旗杆的高度为（）

A . 18米 B . 12米 C . 15米 D . 20米

答案解析收藏纠错 + 选题
7. (2018九上·东台月考) 二次函数 $\text{[math]}$ 的图象经过点(－1，1)，则代数式 $\text{[math]}$ 的值为（）

A . －3 B . －1 C . 2 D . 5

答案解析收藏纠错 + 选题
8. (2018九上·东台月考) 抛物线y=ax²+bx+c（a≠0）图象如图所示，下列结论错误的是（）

A . abc＜0 B . a+c＜b C . b²+8a＞4ac D . 2a+b＞0

答案解析收藏纠错 + 选题

二、填空题

9. (2020九上·保定月考) 如果 $\text{[math]}$ ，那么 $\text{[math]}$ =．

答案解析收藏纠错 + 选题
10. (2018九上·东台月考) 如图，△ABC中，∠BAC=90°，点G是△ABC的重心，如果AG=4，那么BC=.

答案解析收藏纠错 + 选题
11. (2018九上·东台月考) 已知线段MN＝6cm，P是线段MN的一个黄金分割点，则其中较长线段MP的长是.

答案解析收藏纠错 + 选题
12. (2024九下·汝城期末) 在△ABC中，若|cosA- $\text{[math]}$ |+（1-tanB）²=0，则∠C的度数是.

答案解析收藏纠错 + 选题
13. (2018九上·东台月考) 如图所示，在斜坡的顶部有一铁塔AB，B是CD的中点，CD是水平的，在阳光的照射下，塔影DE留在坡面上.已知铁塔底座宽CD=12米，塔影长DE=18米，小明和小华的身高都是1.6米，同一时刻，小明站在点E处，影子在坡面上，小华站在平地上，影子也在平地上，两人的影长分别为2米和1米，那么塔高AB为米。

答案解析收藏纠错 + 选题
14. (2018九上·东台月考) 已知D是等边△ABC边AB上的一点，现将△ABC折叠，使点C与D重合，折痕为EF，点E、F分别在AC和BC上.如图，若AD∶DB=1∶4，则CE∶CF=.

答案解析收藏纠错 + 选题
15. (2018九上·东台月考) 如图，⊙O是等边三角形 $\text{[math]}$ 的外接圆， $\text{[math]}$ 是⊙O上的一个点， $\text{[math]}$ 是 $\text{[math]}$ 延长线上的一个点，且∠ $\text{[math]}$ =∠ $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则线段 $\text{[math]}$ 的长是.

答案解析收藏纠错 + 选题
16. (2018九上·东台月考) 方格纸中每个小正方形的边长都是单位1，△OAB在平面直角坐标系中的位置如图所示.解答问题：
1. （1）请按要求对△ABO作如下变换：
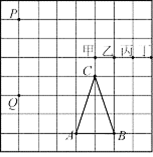
  ①将△OAB向下平移2个单位，再向左平移3个单位得到△O₁A₁B₁；
  
  ②以点O为位似中心，位似比为2：1，将△ABC在位似中心的异侧进行放大得到△OA₂B₂.
2. （2）写出点A₁ ， A₂的坐标：，；
3. （3） △OA₂B₂的面积为.
答案解析收藏纠错 + 选题

三、解答题

17. (2018九上·东台月考)
1. （1）计算：- $\text{[math]}$ tan60°+4sin30°×cos²45°
2. （2）用配方法解方程：x²﹣2x﹣1=0
答案解析收藏纠错 + 选题
18. (2023八下·乾安期末) 射击队为从甲、乙两名运动员中选拔一人参加比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：

第一次
第二次
第三次
第四次
第五次
第六次
平均成绩
中位数
甲
10
8
9
8
10
9
9
①
乙
10
7
10
10
9
8
②
9.5
1. （1）完成表中填空①；②；
2. （2）请计算甲六次测试成绩的方差；
3. （3）若乙六次测试成绩方差为 $\text{[math]}$ ，你认为推荐谁参加比赛更合适，请说明理由．
答案解析收藏纠错 + 选题
19. (2018九上·东台月考) 小颖和小丽做“摸球”游戏：在一个不透明的袋子中装有编号为1~4的四个球（除编号外都相同），从中随机摸出一个球，记下数字后放回，再从中摸出一个球，记下数字。若两次数字之和大于5，则小颖胜，否则小丽胜。这个游戏对双方公平吗？请说明理由。

答案解析收藏纠错 + 选题
20. (2021九上·西岗月考) 如图，△ABC中，∠A=30°，∠B=45°，AC=4，求AB的长.

答案解析收藏纠错 + 选题
21. (2018九上·东台月考) 如图，操场上有一根旗杆AH.为测量它的高度，在B和D处各立一根高1.5米的标杆BC、DE，两杆相距30米，测得视线AC与地面的交点为F，视线AE与地面的交点为G，并且H、B、F、D、G都在同一直线上，测得BF为3米，DG为5米，求旗杆AH的高度?

答案解析收藏纠错 + 选题
22. (2018九上·东台月考) 如图，在△ABC中，AB=AC，以AB为直径的⊙O分别与BC，AC交于点D，E，过点D作⊙O的切线DF，交AC于点F.
1. （1）求证：DF⊥AC；
2. （2）若⊙O的半径为4，∠CDF=22.5°，求阴影部分的面积.
答案解析收藏纠错 + 选题
23. (2018九上·东台月考) 由于雾霾天气对人们健康的影响，市场上的空气净化器成了热销产品.某公司经销一种空气净化器，每台净化器的成本价为200元.经过一段时间的销售发现，每月的销售量y（台）与销售单价x（元）的关系为y＝﹣2x+1000.
1. （1）该公司每月的利润为w元，写出利润w与销售单价x的函数关系式；
2. （2）若要使每月的利润为40000元，销售单价应定为多少元？
3. （3）公司要求销售单价不低于250元，也不高于400元，求该公司每月的最高利润和最低利润分别为多少？
答案解析收藏纠错 + 选题
24. (2018九上·东台月考) 如图，在Rt△ABC中，∠ACB=90°，以BC为半径作⊙B，交AB于点D，交AB的延长线于点E，连接CD、CE.
1. （1）求证：△ACD∽△AEC；
2. （2）当 $\text{[math]}$ 时，求tanE；
3. （3）若AD=4，AC=4 $\text{[math]}$ ，求△ACE的面积.
答案解析收藏纠错 + 选题
25. (2018九上·东台月考) 阅读与应用：
阅读1：a、b为实数，且a＞0，b＞0，因为 $\text{[math]}$ ，所以 $\text{[math]}$ ，从而 $\text{[math]}$ （当a＝b时取等号）．
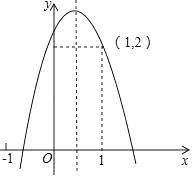
阅读2：函数 $\text{[math]}$ （常数m＞0，x＞0），由阅读1结论可知： $\text{[math]}$ $\text{[math]}$ ，所以当 $\text{[math]}$ 即 $\text{[math]}$ 时，函数 $\text{[math]}$ 的最小值为 $\text{[math]}$ ．
阅读理解上述内容，解答下列问题：
1. （1）问题1：已知一个矩形的面积为4，其中一边长为x，则另一边长为 $\text{[math]}$ ，周长为 $\text{[math]}$ ，求当x＝时，周长的最小值为．
2. （2）问题2：已知函数y₁＝x＋1（x＞－1）与函数y₂＝x²＋2x＋17（x＞－1），当x＝时， $\text{[math]}$ 的最小值为．
3. （3）问题3：某民办学习每天的支出总费用包含以下三个部分：一是教职工工资6400元；二是学生生活费每人10元；三是其他费用．其中，其他费用与学生人数的平方成正比，比例系数为0.01．当学校学生人数为多少时，该校每天生均投入最低？最低费用是多少元？（生均投入＝支出总费用÷学生人数）
答案解析收藏纠错 + 选题
26. (2018九上·东台月考) 已知：如图1，直线 $\text{[math]}$ 与x轴、y轴分别交于点A、C两点，点B的横坐标为2．
1. （1）求A、C两点的坐标和抛物线的函数关系式；
2. （2）点D是直线AC上方抛物线上任意一点，P为线段AC上一点，且S_△_PCD＝2S_△_PAD ，求点P的坐标；
3. （3）如图2，另有一条直线y＝－x与直线AC交于点M，N为线段OA上一点，∠AMN＝∠AOM．点Q为x轴负半轴上一点，且点Q到直线MN和直线MO的距离相等，求点Q的坐标．
答案解析收藏纠错 + 选题