湖北省孝感市云梦县2019届九年级上学期数学期中考试试卷

更新时间：2019-10-15 浏览次数：394 类型：期中考试

一、单选题

1. (2018九上·云梦期中) 小明在解方程x²﹣4x﹣7=0时，他是这样求解的：移项，得x²﹣4x=7，两边同时加4，得x²﹣4x+4=11，∴（x﹣2）²=11，∴x﹣2=± $\text{[math]}$ ，∴x₁=2+ $\text{[math]}$ ，x₂=2﹣ $\text{[math]}$ ，这种解方程的方法称为（）

A . 待定系数法 B . 配方法 C . 公式法 D . 因式分解法

答案解析收藏纠错 + 选题
2. (2018九上·云梦期中) 下列四个图形中，不是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2018九上·云梦期中) 将二次函数 y=x²的图象先向右平移 1 个单位长度，再向下平移 2 个单位长度，可以得到函数（）的图象．

A . y=（x﹣1）²+2 B . y=（x﹣1）²﹣2 C . y=（x+1）²+2 D . y=（x+1）²﹣2

答案解析收藏纠错 + 选题
4. (2018九上·云梦期中) 关于x的一元二次方程（a﹣1）x²+x+a²﹣1=0的一个根是0，则a的值为（）

A . ﹣1 B . 1 C . 1或﹣1 D . 0.5

答案解析收藏纠错 + 选题
5. (2019九上·长春期末) 某药品经过两次降价，每瓶零售价由 156 元降为 118 元．已知两次降价的百分率相同每次降价的百分率为 x，根据题意列方程得（）

A . 156（1+x）²=118 B . 156（1﹣x²）=118 C . 156（1﹣2x）=118 D . 156（1﹣x）²=118

答案解析收藏纠错 + 选题
6. (2018九上·云梦期中) 已知关于 x 的一元二次方程 x²+mx﹣3=0 一个根为 3，则另一个根为（）

A . 1 B . ﹣1 C . 2 D . ﹣6

答案解析收藏纠错 + 选题
7. (2018九上·云梦期中) 如图，在△ABC 中，∠C=90°，∠BAC=70°，将△ABC 绕点 A 顺时针旋转 70°，B，C 旋转后的对应点分别是 B′和 C′，连接 BB′，则∠B′BC′的度数是（）

A . 35° B . 40° C . 50° D . 55°

答案解析收藏纠错 + 选题
8. (2020九上·泉州期中) 在平面直角坐标系中，二次函数 y₁=﹣x²+4x 和一次函数 y₂=2x 的图象如图所示，那么不等式﹣x²+4x＞2x 的解集是（）

A . x＜0 B . 0＜x＜4 C . 0＜x＜2 D . 2＜x＜4

答案解析收藏纠错 + 选题
9. (2018九上·云梦期中) 如图，B，C是⊙A上的两点，AB的垂直平分线与⊙A交于E，F两点，与线段AC交于点D．若∠BFC=18°，则∠DBC=（）

A . 30° B . 32° C . 36° D . 40°

答案解析收藏纠错 + 选题

二、填空题

10. (2018九上·云梦期中) 已知点A（a，1）与点A（4，b）关于原点对称，则a+b＝．

答案解析收藏纠错 + 选题
11. (2018九上·云梦期中) 若方程 x²﹣5x﹣1=0 的两根为 x₁ ， x₂ ，则 x₁·x₂﹣x₁﹣x₂=．

答案解析收藏纠错 + 选题
12. (2018九上·云梦期中) 抛物线y=x²﹣3x﹣15 与x 轴的一个交点是（m，0），则2m²﹣6m 的值为．

答案解析收藏纠错 + 选题
13. (2018九上·云梦期中) 在圆内接四边形ABCD中，∠A、∠B、∠C的度数之比为3：4：6，则∠D=度．

答案解析收藏纠错 + 选题
14. (2018九上·云梦期中) 把二次函数y=（x﹣2）²+1的图象绕原点旋转180°后得到的图象的解析式为．

答案解析收藏纠错 + 选题
15. (2018九上·云梦期中) 如图，在直角坐标系中，已知点 A（﹣3，0），B（0，4），对△OAB 连续作旋转变换，依次得到三角形（1），（2），（3），（4）…，则三角形（2019）的直角顶点的坐标为．

答案解析收藏纠错 + 选题

三、解答题

16. (2018九上·云梦期中) 用指定的方法解下列方程：
1. （1） 2x²﹣3x+1=0（配方法）
2. （2） 4x²﹣4 $\text{[math]}$ x﹣1=0（公式法）
答案解析收藏纠错 + 选题
17. (2019九上·马山期中) 如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为（2，2）请解答下列问题：

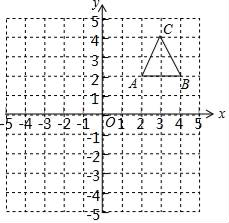
①画出△ABC关于y轴对称的△A₁B₁C₁ ，并写出A₁的坐标．

②画出△ABC绕点B逆时针旋转90°后得到的△A₂B₂C₂ ，并写出A₂的坐标．

③画出△A₂B₂C₂关于原点O成中心对称的△A₃B₃C₃ ，并写出A₃的坐标．

答案解析收藏纠错 + 选题
18. (2018九上·云梦期中) 如图所示的是水面一桥拱的示意图，它的形状类似于抛物线，在正常水位时，该桥下水面宽度为20米，拱顶距离正常水面4米，建立平面直角坐标系如图所示，求抛物线的解析式．

答案解析收藏纠错 + 选题
19. (2018九上·云梦期中) 已知关于x的一元二次方程（x﹣1）（x﹣2）＝m（m+1）
1. （1）试证明：无论m取何值此方程总有两个实数根；
2. （2）若原方程的两根x₁ ， x₂满足x₁²+x₂²﹣x₁x₂＝3m²+2，求m的值．
答案解析收藏纠错 + 选题
20. (2018九上·云梦期中) 如图，已知⊙O 的直径 AB 垂直弦 CD 于点 E，连接 CO 并延长交 AD于点 F，且 CF⊥AD
1. （1）求证：点 E 是 OB 的中点；
2. （2）若 AB=12，求 CD 的长．
答案解析收藏纠错 + 选题
21. (2018九上·云梦期中) 某超市销售樱桃，已知樱桃的进价为14元/千克，如果售价为20元/千克，那么每天可售出 260 千克，如果售价为25元/千克，那么每天可售出210千克，经调查发现：每天的销售量y（千克）与售价 x（元/千克）之间存在一次函数关系
1. （1）求y与x之间的函数关系式；
2. （2）若该超市每天要获得利润 1920 元，同时又要让消费者得到实惠，则售价 x应定于多少元？
3. （3）若樱桃的售价不得高于 28 元/千克，请问售价定为多少时，该超市每天销售樱桃所获的利润最大？最大利润是多少元？
答案解析收藏纠错 + 选题
22. (2020九上·安阳期中) 如图
1. （1）问题发现：
  如图①，△ABC 和△AED 都是等腰直角三角形，∠BAC=∠EAD=90°，点 B 在线段AE 上，点 C 在线段AD 上，请直接写出线段 BE 与线段 CD 的数量与位置关系是关系：；
2. （2）操作探究：
  如图②，将图①中的△ABC 绕点 A 顺时针旋转α（0°＜α＜360°），（1）小题中线段 BE 与线段 CD 的关系是否成立？如果不成立，说明理由，如果成立，请你结合图②给出的情形进行证明；
3. （3）解决问题：
  将图①中的△ABC 绕点 A 顺时针旋转α（0°＜α＜360°），若 DE=2AC，在旋转的过程中，当以 A、B、C、D 四点为顶点的四边形是平行四边形时，在备用图中画出其中的一个情形，并写出此时旋转角α的度数是度．
答案解析收藏纠错 + 选题
23. (2023九上·新会期末) 如图，抛物线y=﹣ $\text{[math]}$ x²+mx+n与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知A（﹣1，0），C（0，2）．
1. （1）求抛物线的表达式；
2. （2）在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明理由；
3. （3）点E时线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF的最大面积及此时E点的坐标．
答案解析收藏纠错 + 选题