浙江省杭州市余杭区2020届九年级上学期数学第一次月考试卷

更新时间：2024-07-13 浏览次数：249 类型：月考试卷

一、选择题（每小题3分，共30分）

1. (2024七下·月湖期末) 不透明袋子中有除颜色外完全相同的4个黑球和2个白球，从袋子中随机摸出3个球，下列事件是必然事件的是（）．

A . 3个都是黑球 B . 2个黑球1个白球 C . 2个白球1个黑球 D . 至少有1个黑球

答案解析收藏纠错 + 选题
2. (2019九上·余杭月考) 箱子内装有53颗白球及2颗红球，小芬打算从箱子内抽球，以毎次抽出一球后将球再放回的方式抽53次球.若箱子内每颗球被抽到的机会相等，且前52次中抽到白球51次及红球1次，则第53次抽球时，小芬抽到红球的机率为何？（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021九上·贵州期中) 在平面直角坐标系中，抛物线y=(x+5）（x-3）经变换后得到抛物线y=（x+3）（x-5），则这个变换可以是（）

A . 向左平移2个单位 B . 向右平移2个单位 C . 向左平移8个单位 D . 向右平移8个单位

答案解析收藏纠错 + 选题
4. (2020九上·瑶海月考) 在平面直角坐标系中，已知a≠b，设函数y=（x+a）（x+b）的图象与x轴有M个交点，函数y=（ax+1）（bx+1）的图象与x轴有N个交点，则（）

A . M=N-1或M=N+1 B . M=N-1或M=N+2 C . M=N或M=N+1 D . M=N或M=N-1

答案解析收藏纠错 + 选题
5. (2019九上·余杭月考) 已知抛物线 $\text{[math]}$ 与y轴交于点A ，与直线 $\text{[math]}$ （k为任意实数）相交于B ， C两点，则下列结论错误的是（）

A . 存在实数k ，使得 $\text{[math]}$ 为等腰三角形 B . 存在实数k ，使得 $\text{[math]}$ 的内角中有两角分别为30°和60° C . 任意实数k ，使得 $\text{[math]}$ 都为直角三角形 D . 存在实数k ，使得 $\text{[math]}$ 为等边三角形

答案解析收藏纠错 + 选题
6. (2019九上·余杭月考) 有三条带子，第一条的一头是黑色，另一头是黄色，第二条的一头是黄色，另一头是白色，第三条的一头是白色，另一头是黑色．若任意选取这三条带子的一头，颜色各不相同的概率是（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2019九上·余杭月考) 下列说法正确的是（　　）.
①试验条件不会影响某事件出现的频率；
②在相同的条件下试验次数越多，就越有可能得到较精确的估计值，但各人所得的值不一定相同；
③如果一枚骰子的质量分布均匀，那么抛掷后每个点数出现的机会均等；
④抛掷两枚质量分布均匀的相同的硬币，出现“两个正面”、“两个反面”、“一正一反”的机会相同．

A . ①② B . ②③ C . ③④ D . ①③

答案解析收藏纠错 + 选题
8. (2019九上·余杭月考) 义乌国际小商品博览会某志愿小组有五名翻译，其中一名只会翻译阿拉伯语，三名只会翻译英语，还有一名两种语言都会翻译.若从中随机挑选两名组成一组，则该组能够翻译上述两种语言的概率是（）.

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2019九上·余杭月考) 如图，抛物线 $\text{[math]}$ 交x轴于点A，B，交y轴于点C，当△ABC纸片上的点C沿着此抛物线运动时，则△ABC纸片随之也跟着水平移动，设纸片上BC的中点M坐标为(m，n)，在此运动过程中，n与m的关系式是（）

A . n= $\text{[math]}$ (m- $\text{[math]}$ )²- $\text{[math]}$ B . n= $\text{[math]}$ (m- $\text{[math]}$ )²+ $\text{[math]}$ C . n= $\text{[math]}$ (m- $\text{[math]}$ )²- $\text{[math]}$ D . n= $\text{[math]}$ (m- $\text{[math]}$ )²- $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2019九上·余杭月考) 四位同学在研究函数y₁＝ax²＋ax－2a (a是非零常数)时，甲发现该函数图象总经过定点；乙发现若抛物线y₁＝ax²＋ax－2a总不经过点P(x₀－3，x₀²－16)，则符合条件的点P有且只有2个；丙发现若直线y₂＝kx＋b与函数y₁交于x轴上同一点，则b＝－k；丁发现若直线y₃＝m (m≠0)与抛物线有两个交点(x₁ ， y₁)(x₂ ， y₂)，则x₁＋x₂＋1＝0.已知这四位同学中只有一位发现的结论是错误的，则该同学是（）

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题

二、填空题（每小题4分，共24分）

11. (2019九上·余杭月考) 一口袋中有6个红球和若干个白球，除颜色外均相同，从口袋中随机摸出一球，记下颜色，再把它放回口袋中摇匀．重复上述实验共300次，其中120次摸到红球，则口袋中大约有个白球．

答案解析收藏纠错 + 选题
12. (2024九上·龙岗期末) 将长度为8厘米的木棍截成三段，每段长度均为整数厘米．如果截成的三段木棍长度分别相同算作同一种截法（如：5，2，1和1，5，2），那么截成的三段木棍能构成三角形的概率是．

答案解析收藏纠错 + 选题

13. (2019九上·余杭月考) 已知二次函数y=ax²+bx﹣3自变量x的部分取值和对应函数值y如下表：

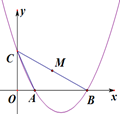
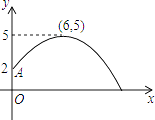
则在实数范围内能使得y﹣5＞0成立的x取值范围是.

x	…	﹣2	﹣1	0	1	2	3	…
y	…	5	0	﹣3	﹣4	﹣3	0	…

答案解析收藏纠错 + 选题

14. (2019九上·余杭月考) 直线y=ax+m和直线y=bx+n在同一平面直角坐标系中的图象如图所示，则抛物线y=ax²+bx+c的对称轴为．

答案解析收藏纠错 + 选题
15. (2019九上·余杭月考) 某一房间内A、B两点之间设有探测报警装置，小车（不计大小）在房间内运动，当小车从AB之间经过时，将触发报警.现将A、B两点放置于平面直角坐标系xOy中（如图）已知点A，B的坐标分别为（0，4），（5，4），小车沿抛物线y=ax²-2ax-3a运动.若小车在运动过程中只触发一次报警，则a的取值范围是

答案解析收藏纠错 + 选题
16. (2020九上·营口期中) 如图，抛物线y＝ax²+bx+c（a≠0）的对称轴为直线x＝1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：
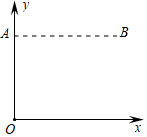
①4ac＜b²；

②方程ax²+bx+c＝0的两个根是x₁＝﹣1，x₂＝3；

③3a+c＞0；

④当y＞0时，x的取值范围是﹣1≤x＜3；

⑤当x＜0时，y随x增大而增大；

其中结论正确有.

答案解析收藏纠错 + 选题

三、解答题（本大题有7小题，共66分）

17. (2019九上·余杭月考) 某商场搞摸奖促销活动，商场在一只不透明的箱子里放了三个相同的小球，球上分别写有“10元”、“20元”、“30元”的字样，规定：顾客在本商场同一日内，每消费满100元，就可以在这只箱子里摸出一个小球（顾客每次摸出小球看过后仍然放回箱内搅匀），商场根据顾客摸出小球上所标金额就送上一份相应价格的奖品．现有一顾客在商场一次性消费了215元，按规定，该顾客可以摸奖两次，求该顾客两次摸奖所获奖品的价格之和超过40元的概率．

答案解析收藏纠错 + 选题
18. (2022·绍兴模拟) 某校组织一项公益知识竞赛，比赛规定：每个班级由2名男生、2名女生及1名班主任老师组成代表队．但参赛时，每班只能有3名队员上场参赛，班主任老师必须参加，另外2名队员分别在2名男生和2名女生中各随机抽出1名．初三（1）班由甲、乙2名男生和丙、丁2名女生及1名班主任组成了代表队，求恰好抽到由男生甲、女生丙和这位班主任一起上场参赛的概率．（请用“画树状图”或“列表”或“列举”等方法给出分析过程）

答案解析收藏纠错 + 选题
19. (2023九上·越城月考) 如图，用长为6m的铝合金条制成“日”字形窗框，若窗框的宽为x m，窗户的透光面积为y m²（铝合金条的宽度不计）．
1. （1）求出y与x的函数关系式；
2. （2）如何安排窗框的长和宽，才能使得窗户的透光面积最大？并求出此时的最大面积．
答案解析收藏纠错 + 选题
20. (2019九上·余杭月考) 在体育测试时，九年级的一名高个男同学推铅球，已知铅球所经过的路径是某个二次函数图象的一部分（如图所示）.如果这个男同学出手处A点的坐标是（0，2），铅球路线的最高处B点的坐标是（6，5）.求这个二次函数的解析式.

答案解析收藏纠错 + 选题
21. (2019九上·余杭月考) 某公司准备投资开发A、B两种新产品，通过市场调研发现：如果单独投资A种产品，则所获利润y_A（万元）与投资金额x（万元）之间满足正比例函数关系：y_A=kx；如果单独投资B种产品，则所获利润y_B（万元）与投资金额x（万元）之间满足二次函数关系：y_B=ax²+bx．根据公司信息部的报告，y_A、y_B（万元）与投资金额x（万元）的部分对应值（如下表）
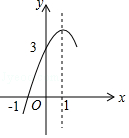
x
1
5
y_A
0.6
3
y_B
2.8
10
1. （1）求正比例函数和二次函数的解析式；
2. （2）如果公司准备投资20万元同时开发A、B两种新产品，请你设计一个能获得最大利润的投资方案，并求出按此方案能获得的最大利润是多少万元？
答案解析收藏纠错 + 选题
22. (2019九上·余杭月考) 如图，在平面直角坐标系中，抛物线y=x²+mx+n经过点A（3，0）、B（0，-3），点P是直线AB上的动点，过点P作x轴的垂线交抛物线于点M ，设点P的横坐标为t ．
1. （1）分别求出直线AB和这条抛物线的解析式．
2. （2）若点P在第四象限，连接AM、BM ，当线段PM最长时，求△ABM的面积．
3. （3）是否存在这样的点P ，使得以点P、M、B、O为顶点的四边形为平行四边形？若存在，请直接写出点P的横坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题
23. (2020·临海模拟) 如图，抛物线y＝﹣x²+bx+c与x轴交于点A（﹣2，0）和B（l，0），与y轴交于点C.
1. （1）求抛物线的表达式；
2. （2）作射线AC，将射线AC绕点A顺时针旋转90°交抛物线于另一点D，在射线AD上是否存在一点H，使△CHB的周长最小.若存在，求出点H的坐标；若不存在，请说明理由；
3. （3）在（2）的条件下，点Q为抛物线的顶点，点P为射线AD上的一个动点，且点P的横坐标为t，过点P作x轴的垂线l，垂足为E，点P从点A出发沿AD方向运动，直线l随之运动，当﹣2＜t＜1时，直线l将四边形ABCQ分割成左右两部分，设在直线l左侧部分的面积为S，求S关于t的函数表达式.
答案解析收藏纠错 + 选题