如图所示,有一斜面倾角为θ、质量为M的斜面体置于水平面上,A是最高点,B是最低点,C是AB的中点,其中AC段光滑、CB段粗糙.一质量为m的小滑块由A点静止释放,经过时间t滑至C点,又经过时间t到达B点.斜面体始终处于静止状态,取重力加速度为g,则( )

如图所示,倾角为θ=30°的光滑绝缘直角斜面ABC,D是斜边AB的中心,在C点固定一个带电荷量为+Q的点电荷.一质量为m,电荷量为﹣q的小球从A点由静止释放,小球经过D点时的速度为v,到达B点时的速度为0,则( )

某缓冲装置的理想模型如图所示,劲度系数足够大的轻质弹簧与轻杆相连,轻杆可在固定的竖直槽内移动,与槽间的滑动摩擦力恒为Ff , 轻杆向下移动不超过l时,装置可安全工作.一质量为m的重物若从离弹簧上端h高处由静止自由下落碰撞弹簧,将导致轻杆向下移动了 .轻杆与槽间的最大静摩擦力等于滑动摩擦力,且不计小车与地面的摩擦.已知重力加速度为g.

如图所示,一物体质量m=2kg,在倾角θ=37°的斜面上的A点以初速度v0=3m/s下滑,A点距弹簧上端B的距离AB=4m,当物体到达B后将弹簧压缩到C点,最大压缩量BC=0.2m,然后物体又被弹簧弹上去,弹到的最高位置为D点,D点距A点AD=3m,挡板及弹簧质量不计,g取10m/s2 . 求:

如图,两足够长的平行粗糙金属导轨MN,PQ相距d=0.5m.导轨平面与水平面夹角为α=30°,处于方向垂直导轨平面向上、磁感应强度B=0.5T的匀强磁场中,长也为d的金属棒ab垂直于导轨MN、PQ放置,且始终与导轨接触良好,导体棒质量m=0.1kg,电阻R=0.lΩ,与导轨之间的动摩擦因数μ= ,导轨上端连接电路如图,已知电阻R1与灯泡电阻RL的阻值均为0.2R,导轨电阻不计,取重力加速度大小g=10m/s2 ,

如图所示,区域Ⅰ、Ⅲ内存在垂直纸面向外的匀强磁场,区域Ⅲ内磁场的磁感应强度B,宽为1.5d,区域Ⅰ中磁场的磁感应强度B1未知,区域Ⅱ时无场区,宽为d.一个质量为m,电荷量为q的带正电粒子从磁场边界上的A点与边界成θ=60°角垂直射入区域Ⅰ的磁场,粒子恰好不从区域Ⅲ的右边界穿出且刚好能回到A点,粒子重力不计,求:

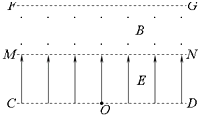
如图所示,虚线FG、MN、CD为在同一平面内的水平直线边界,在MN、CD间有垂直边界的匀强电场,场强的大小E=1.5×105N/C,方向如图,在FG、MN间有垂直于纸面向外的匀强磁场,磁感应强度大小B=0.2T,已知电场和磁场沿边界方向的长度均足够长,电场在垂直边界方向的宽度d1=0.20m,在CD边界上某点O处有一放射源,沿纸面向电场中各个方向均匀地辐射出速率均为v0=1.0×106m/s的某种带正电粒子,粒子质量m=6.4×10﹣27kg,电荷量q=3.2×10﹣19C,粒子可以无阻碍地通过边界MN进入磁场,不计粒子的重力及相互作用.