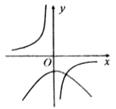
一、选择题(本大题共10小题,每小题4分,满分40分.)
-
A . y=x2-x(x+2)
B . y=x2-  C . x=y2
D . y=(x-1)(x+3)
C . x=y2
D . y=(x-1)(x+3)
-
A . k<  B . k>
B . k>  C . k>2
D . k<2
C . k>2
D . k<2
-
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
-
A . 先向左平移5个单位长度,再向下平移1个单位长度
B . 先向左平移5个单位长度,再向上平移1个单位长度
C . 先向右平移5个单位长度,再向下平移1个单位长度
D . 先向右平移5个单位长度,再向上平移1个单位长度
-
A . 24
B . 36
C . 48
D . 96
-
A . 当x=2时,y有最大值5
B . 当x=-1时,y有最小值-22
C . 当x=-1时,y有最大值32
D . 当x=1时,y有最小值2
-
A . 该函数图象的开口向下
B . 该函数图象的顶点坐标是(-2,-7)
C . 当x<0时,y随x的增大而增大
D . 该函数图象与x轴有两个不同的交点,且分布在坐标原点两侧
-
8.
(2019九上·利辛月考)
若点(-3,y
1)、(1,y
2)、(3,y
3)都在二次函数y=(x+1)
2+k的图象上,则y
1 , y
2 , y
3的大小关系是( )
A . y1< y2<y3
B . y1=y3>y2
C . y1=y2 <y3
D . y1= y2>y3
-
9.
(2019九上·利辛月考)
二次函数y=-kx
2-k
2与反比例函数y=

(k≠0)在同一平面直角坐标系内的大致图象可能是( )
-
10.
(2019九上·利辛月考)
二次函数y=ax
2+bx+c(a≠0)的部分图象如图所示,图象过点(-4,0),对称轴为直线x=-1,下列结论:①abc>0;②2a-b=0;③一元二次方程ax
2+bx+c=0的解是x
1=-4,x
2=1;④当y>0时,-4<x<2,其中正确的结论有( )
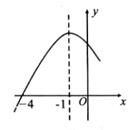
A . 4个
B . 3个
C . 2个
D . 1个
二、填空题(本大题共4小题,每小题5分,满分20分)
-
-
12.
(2019九上·利辛月考)
据权威部门发布的消息,2019年第一季度安徽省城镇居民人均可支配收入约为0.75万元,若第三季度安徽省城镇居民人均可支配收入为y万元,平均每个季度城镇居民人均可支配收入增长的百分率为x,则y与x之间的函数表达式是
。
-
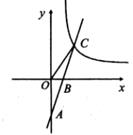
13.
(2019九上·利辛月考)
如图,一次函数y=ax+b的图象交x轴于点B,交y轴于点A,交反比例函数y=

的图象于点C,若AB=BC,且△OBC的面积为2,则k的值为
。
-
14.
(2019九上·利辛月考)
在平面直角坐标系中,函数y=-x+3a+2(a≠0)和y=x
2-ax的图象相交于P,Q两点若P,Q都在x轴的上方,则实数a的取值范围是
。
三、解答题(本大题共2小题,每小题8分,满分16分)
-
-
16.
(2019九上·利辛月考)
有三位同学分别说出了二次函数的图象与性质:
甲:抛物线的开口向上;
乙:抛物线与x轴没有交点;
丙:当x>-2时,y随x的增大而增大。
请写出一个符合上述条件的二次函数表达式。
四、计算题(本大题共2小题,每小题8分,满分16分)
-
-
18.
(2019九上·利辛月考)
下表给出了两个变量x,y的部分对应值
| x | … | 0.5 | 1 | 1.5 | 2 | 3 | 4 | 6 | 8 | … |
| y | … | 12 | 6 | 4 | 3 | 2 | 1.5 | 1 | 0.75 | … |
-
(1)
以表中x的值为横坐标,对应的y的值为纵坐标,在给出的平面直角坐标系中描点;
-
(2)
选用一个你学过的函数来描述两个变量x,y之间的关系,并确定其函数表达式.
五、综合题
-
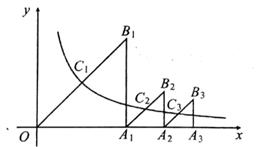
19.
(2019九上·利辛月考)
如图,△OA
1B
1 , △A
1A
2B
2 , △A
2A
3B
3 , …是分别以A
1 , A
2 , A
3 , …为直角顶点,一条直角边在x轴正半轴上的等腰直角三角形,其斜边的中点C
1(x
1 , y
1),C
2(x
2 , y
2),C
3(x
3 , y
3),均在反比例函数y=

(x>0)的图象上,易求得y
1=2;y
2=2

-2;y
3=2

-2

;
-
-
(2)
根据上述规律猜想:yn=(n是正整数,用含n的式子表示,不用说理);
-
(3)
利用(2)的结论求y1+y2+…+y10的值
-
-
(1)
求证:无论k为何值,该二次函数的图象与x轴都有交点;
-
(2)
若该函数图象的顶点在坐标轴上,试确定k的值。
-
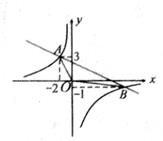
21.
(2019九上·利辛月考)
如图,一次函数y
1=ax+b的图象和反比例函数y
2=

的附象相交于A(-2,3)和B(m,-1)两点。
-
-
-
(3)
结合图象,直接写出使y1>y2成立的x的取值范围。
-
22.
(2019九上·利辛月考)
某公司研制出新产品,该产品的成本为每件2400元.在试销期间,购买不超过10件时,每件销售价为3000元;购买超过10件时,每多购买一件,所购产品的销售单价均降低5元,但最低销售单价为2600元。请解决下列问题:
-
(1)
直接写出:购买这种产品 件时,销售单价恰好为2600元;
-
(2)
设购买这种产品x件(其中x>10,且x为整数),该公司所获利润为y元,求y与x之间的函数表达式;
-
(3)
该公司的销售人员发现:当购买产品的件数超过10件时,会出现随着数量的增多,公司所获利润反而减少这一情况.为使购买数量越多,公司所获利润越大,公司应将最低销售单价调整为多少元?(其它销售条件不变)
-
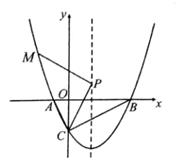
-
-
(2)
若该抛物线与x轴交于点A,B(点A在点B的左侧),与y轴交于点C。
①试判断△ABC的形状,并说明理由;
②在该抛物线的对称轴上是否存在点P,使PM+PC的值最小?若存在,求出它的最小值;若不存在,请说明理由。
 B .
B . 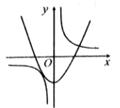 C .
C .  D .
D .