广东省湛江市霞山职业高级中学2020-2021学年九年级上学...

更新时间：2020-12-10 浏览次数：188 类型：期中考试

一、单选题（共10题；共30分）

1. (2020九上·湛江期中) 二次函数 $\text{[math]}$ 图像的开口方向是（）．

A . 向上 B . 向下 C . 向左 D . 向右

答案解析收藏纠错 + 选题
2. (2020九上·孝南期中) 若点 $\text{[math]}$ 与 $\text{[math]}$ 关于原点对称，则直线 $\text{[math]}$ 不经过（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
3. (2020九上·湛江期中) 关于x的一元二次方程 $\text{[math]}$ 的一个根0，则a值为（）

A . 2 B . -2 C . ±2 D . 0

答案解析收藏纠错 + 选题
4. (2020九上·湛江期中) 函数 $\text{[math]}$ 与y=-mx²+m(m≠0)在同一直角坐标系中的大致图像可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2024九上·曲靖期末) 下列关于数字变换的图案中，是中心对称图形但不是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2020九上·湛江期中) 如图，⊙O是△ABC的外接圆，半径为2cm ，若BC＝2cm ，则∠A的度数为（）

A . 30° B . 25° C . 15° D . 10°

答案解析收藏纠错 + 选题
7. (2020九上·湛江期中) 如图，AB为⊙O的直径，点D是弧AC的中点，过点D作DE⊥AB于点E，延长DE交⊙OO于点F，若AC = 12，AE = 3，则⊙O的直径长为（　　　）

A . 10 B . 13 C . 15 D . 16

答案解析收藏纠错 + 选题
8. (2020九上·湛江期中) 如图，AB，AC，BD是⊙O的切线，切点分别是P，C，D.若AC=5，BD=3，则AB的长是（　　）

A . 2 B . 4 C . 6 D . 8

答案解析收藏纠错 + 选题
9. (2022九上·晋江期末) 如图所示，在半径为10cm的⊙O中，弦AB＝16cm ， OC⊥AB于点C ，则OC等于（　　）

A . 3cm B . 4cm C . 5cm D . 6cm

答案解析收藏纠错 + 选题
10. (2020九上·湛江期中) 如图，等边 $\text{[math]}$ 的边长为 $\text{[math]}$ ，以O为圆心， CD为直径的半圆经过点A，连接 AD， BC相交于点P，将等边 $\text{[math]}$ 从 OA与 OC重合的位置开始，绕着点O顺时针旋转 120°，交点P运动的路径长是( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（共7题；共28分）

11. (2022九上·义乌月考) 二次函数 $\text{[math]}$ 图像的顶点坐标是.

答案解析收藏纠错 + 选题
12. (2020九上·湛江期中) 已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点都在抛物线 $\text{[math]}$ 上，比较 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的大小．（用“<”连接）

答案解析收藏纠错 + 选题
13. (2020九上·湛江期中) 直线 $\text{[math]}$ 与抛物线 $\text{[math]}$ 如图所示，当 $\text{[math]}$ > $\text{[math]}$ 时，x的取值范围是．

答案解析收藏纠错 + 选题
14. (2023八下·灌南期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ .将 $\text{[math]}$ 绕点B逆时针旋转60°，得到 $\text{[math]}$ ，则 $\text{[math]}$ 边的中点D与其对应点 $\text{[math]}$ 的距离是.

答案解析收藏纠错 + 选题
15. (2020九上·湛江期中) 如图，在平面直角坐标系中，已知点A （0，1）、B（0，1+t）、C（0，1-t）（t＞0），点P在以D（4，4）为圆心，1为半径的圆上运动，且始终满足∠BPC=90°，则t的取值范围是。

答案解析收藏纠错 + 选题
16. (2020九上·湛江期中) 如图，点A，B，C，D都在⊙O上，弧CD 的度数等于84°，CA是∠OCD的平分线，则∠ABD+∠CAO=°

答案解析收藏纠错 + 选题
17. (2021九上·河南月考) 二次函数y＝ax²＋bx＋c（a≠0）的图象如图所示，对称轴为直线x＝－1，下列结论：① b²＞4ac；② abc＞0；③ a－c＜0；④ am²＋bm≥a－b（m为任意实数），其中正确的结论是

答案解析收藏纠错 + 选题

三、解答题（一）（共3题；共18分）

18. (2021九上·武汉月考) 解方程：x²﹣3x﹣2＝0．

答案解析收藏纠错 + 选题
19. (2020九上·湛江期中) 已知函数y=2x²-(3-k)x+k²-3k-10的图象经过原点，试确定k的值。

答案解析收藏纠错 + 选题
20. (2020九上·湛江期中) 如图，在平面直角坐标系xOy中，△ABC的三个顶点坐标分别为A（1，1），B（4，0），C（4，4）
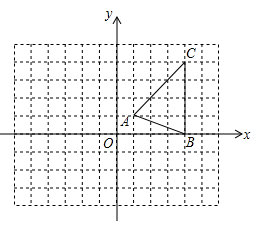
按下列要求作图：

①将△ABC向左平移4个单位，得到△A₁B₁C₁ ，并写出A₁ ， B₁ ， C₁的坐标。

②将△A₁B₁C₁绕点B₁逆时针旋转90°，得到△A₂B₂C₂；并写出A₂ ， C₂的坐标。

答案解析收藏纠错 + 选题

四、解答题（二）（共3题；共24分）

21. (2020九上·湛江期中) 如图，已知抛物线 $\text{[math]}$ 与y轴交于点C(0，-5)，与轴交于点A和点B，其中点B的坐标为(5，0)抛物线对称轴为直线x=2．
1. （1）求抛物线的解析式；
2. （2）当 $\text{[math]}$ 时，y的取值范围为．
3. （3）点P为该二次函数在第四象限内图像上的一动点，过点P作 $\text{[math]}$ 轴，交于点Q，设线段PQ长为l，求l的最大值，并写出此时点P的坐标．
答案解析收藏纠错 + 选题
22. (2020九上·湛江期中) 某水果批发商销售每箱进价为40元的苹果，物价部门规定每箱售价不得高于55元，市场调查发现：若每箱以50元的价格出售，平均每天销售80箱，价格每提高1元，平均每天少销售2箱．
1. （1）求平均每天销售量y（箱）与销售价x（元/箱）之间的函数关系式；
2. （2）求该批发商平均每天的销售利润W（元）与销售价x（元/箱）之间的函数关系式；
3. （3）当每箱苹果的销售价为多少元时，可以获得最大利润？最大利润是多少？
答案解析收藏纠错 + 选题
23. (2020九上·湛江期中) 如图，在△ABC中，BC＝4，且△ABC的面积为4，以点A为圆心，2为半径的⊙A交AB于E，交AC于F，点P是⊙A上一点，且∠EPF＝45°．
1. （1）求证：BC为⊙A的切线；
2. （2）求图中阴影部分的面积．
答案解析收藏纠错 + 选题

五、综合题（共2题；共20分）

24. (2020九上·湛江期中) 综合与探究
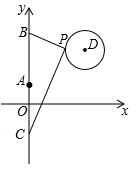
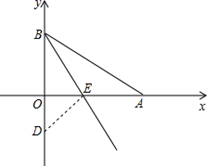
如图，在平面直角坐标系中，点A、B分别在x轴y轴的正半轴上，线段OA的长是不等式 $\text{[math]}$ 的最大整数解，线段OB的长是一元二次方程 $\text{[math]}$ 的一个根，将 $\text{[math]}$ 沿BE折叠，使AB边落在OB边所在的y轴上，点A与点D重合．
1. （1）求OA、OB的长；
2. （2）求直线BE的解析式；
3. （3）在平面内是否存在点M，使B、O、E、M为顶点的四边形为平行四边形？若存在，请直接写出点M的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题
25. (2020九上·湛江期中) 如图，在正方形ABCD中，点E，F分别是CD，AD的中点，BE与CF相交于点P.
1. （1）求证：BE⊥CF.
2. （2）若AB＝a.
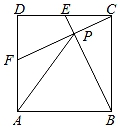
  ①求CP和AP的长（用含a的代数式表示）.
  
  ②连结DP，直接写出∠DPF的度数.
答案解析收藏纠错 + 选题