月用水量(吨) | 5 | 6 | 7 | 8 | 9 | 10 |
户数 | 1 | 1 | 2 | 2 | 3 | 1 |
则这10户家庭的月用水量的平均数和众数分别是( )

已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).设四边形APFE的面积为y(cm2),则下列图象中,能表示y与t的函数关系的图象大致是( )

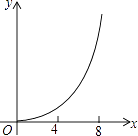 B .
B .  C .
C .  D .
D . 
某中学初三年级的学生开展测量物体高度的实践活动,他们要测量一幢建筑物AB的高度.如图,他们先在点C处测得建筑物AB的顶点A的仰角为30°,然后向建筑物AB前进10m到达点D处,又测得点A的仰角为60°,那么建筑物AB的高度是 m.


为了响应市政府“绿色出行”的号召,小张上下班由自驾车方式改为骑自行车方式.已知小张单位与他家相距20千米,上下班高峰时段,自驾车的平均速度是自行平均车速度的2倍,骑自行车所用时间比自驾车所用时间多 小时.求自驾车平均速度和自行车平均速度各是多少?



上课时李老师提出这样一个问题:对于任意实数x,关于x的不等式x2﹣2x﹣1﹣a>0恒成立,求a的取值范围.
小捷的思路是:原不等式等价于x2﹣2x﹣1>a,设函数y1=x2﹣2x﹣1,y2=a,画出两个函数的图象的示意图,于是原问题转化为函数y1的图象在y2的图象上方时a的取值范围.
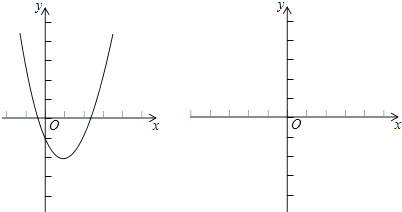
对于任意实数x,关于x的不等式x2﹣2x﹣1﹣a>0恒成立,则a的取值范围是 .
关于x的方程x﹣4= 在0<a<4范围内有两个解,求a的取值范围.
正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图2.
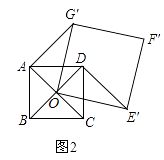
①在旋转过程中,当∠OAG′是直角时,求α的度数;
②若正方形ABCD的边长为1,在旋转过程中,求AF′长的最大值和此时α的度数,直接写出结果不必说明理由.
“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”S=ah.
例如:三点坐标分别为A(1,2),B(﹣3,1),C(2,﹣2),则“水平底”a=5,“铅垂高”h=4,“矩面积”S=ah=20.
①若A,B,P三点的“矩面积”为12,求点P的坐标;
②直接写出A,B,P三点的“矩面积”的最小值.
①若E,F,M三点的“矩面积”为8,求m的取值范围;
②直接写出E,F,N三点的“矩面积”的最小值及对应n的取值范围.