吉林省长春市朝阳区2019-2020学年九年级上学期数学期中...

更新时间：2024-07-13 浏览次数：490 类型：期中考试

一、选择题(每小题3分，共24分)

1. (2019九上·朝阳期中) 一元二次方程x²-x-4=0的一次项系数和常数项分别是（）

A . 1，-1 B . 1，-4 C . -1，-4 D . -1，4

答案解析收藏纠错 + 选题
2. (2023九上·二道期中) 下列二次根式中，是最简二次根式的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2019九上·朝阳期中) 若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2019九上·朝阳期中) 一元二次方程x²+4x+2=0的根的判别式的值为（）

A . 8 B . 24 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2020·福州模拟) 若二次根式 $\text{[math]}$ 在实数范围内有意义，则x的取值范围在数轴上表示正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2019九上·朝阳期中) 如图，以点O为位似中心，把△ABC放大为原图形的2倍得到△A'B'C'，下列说法中正确的是（）

A . OA：OA'=1：3 B . OA：AA'=1：2 C . OA：AA'=1：3 D . OA'：AA'=1：3．

答案解析收藏纠错 + 选题
7. (2019九上·朝阳期中) 《孙子算经》是中国古代重要的数学著作，成书于约一千五百年前。其中有首歌谣：今有竿不知其长，量得影长一丈五尺，立一标杆，长一尺五寸，影长五寸，问竿长几何？意即：有一根竹竿不知道有多长，量出它在太阳下的影子长丈五尺．同时立一根一尺五寸的小标杆，它的影长五寸(提示：1丈=10尺，1尺=10寸)，则竹竿的长为（）

A . 五丈 B . 四丈五尺 C . 一丈 D . 五尺

答案解析收藏纠错 + 选题
8. (2019九上·朝阳期中) 如图，P是 $\text{[math]}$ ABCD内一点，连结P与 $\text{[math]}$ ABCD各顶点， $\text{[math]}$ EFGH各顶点分别在边AP、BP、CP、DP上，且AE=2EP，EF∥AB．若△PEF与△PGH的面积和为1，则 $\text{[math]}$ ABCD的面积为（）

A . 4 B . 6 C . 12 D . 18

答案解析收藏纠错 + 选题

二、填空题(每小题3分，共18分)

9. (2024八上·房山期中) 计算：( $\text{[math]}$ )²=。

答案解析收藏纠错 + 选题
10. (2019九上·朝阳期中) 一元二次方程x²-3x=0的较大的根为。

答案解析收藏纠错 + 选题
11. (2019九上·朝阳期中) 北京市为了全民健身，举办“健步走”活动；活动路线为玲珑塔→国家体育场→水立方。如果体育局的工作人员在设计图上标记玲珑塔的坐标为(0，1)，国家体育场的坐标为(1，0)，则终点水立方的坐标是。

答案解析收藏纠错 + 选题
12. (2019九上·朝阳期中) 如图，AB∥CD∥EF，直线l₁、l₂与这三条平行线分别交于点A、D、F和点B、C、E．若AD：DF=3：1，BE=10，则CE的长为。

答案解析收藏纠错 + 选题
13. (2019九上·朝阳期中) 如图是测量玻璃管内径的示意图，点D正对10mm刻度线，点A正对30mm刻度线，DE∥AB．若量得AB的长为6mm，则内径DE的长为mm。

答案解析收藏纠错 + 选题
14. (2019九上·朝阳期中) 两个等腰直角三角板如图放置，点D为AB的中点．若AG=3，CG=1，则点G、H之间的距离为。

答案解析收藏纠错 + 选题

三、解答题(本大题10小题，共78分)

15. (2019九上·朝阳期中) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
16. (2019九上·朝阳期中) 用配方法解方程：x²-4x-1=0

答案解析收藏纠错 + 选题
17. (2019九上·朝阳期中) 小明在解方程x²-5x=1时出现了错误，解答过程如下：
∵a=1，b=-5，c=1，（第一步）

∴b²-4ac=(-5)²-4×1×1=21（第二步）

∴x= $\text{[math]}$

∴x₁= $\text{[math]}$ ，x₂= $\text{[math]}$ (第四步)
1. （1）小明解答过程是从第步开始出错的，其错误原因是。
2. （2）写出此题正确的解答过程。
答案解析收藏纠错 + 选题
18. (2019九上·朝阳期中) 已知关于x的一元二次方程x²+(k+1)x+ $\text{[math]}$ k²=0有两个不相等的实数根。
1. （1）求k的取值范围。
2. （2）当k取最小整数时，求方程的解。
答案解析收藏纠错 + 选题
19. (2019九上·朝阳期中) 如图①、图②、图③，在4×4的正方形网格中，每个小正方形的边长为1，每个小正方形的顶点叫做格点，线段AB的端点都在格点上，请仅用无刻度的直尺，分别按下列要求画图，保留作图痕迹。
1. （1）在图①中找到格点C、D，使得AC∥BD，且 $\text{[math]}$
2. （2）在图②中的线段AB上找到点E，使得 $\text{[math]}$
3. （3）在图③中的线段AB上找到点F，使得 $\text{[math]}$
答案解析收藏纠错 + 选题
20. (2019九上·朝阳期中) 如图，△ABC的中线BD、CE相交于点O，F、G分别是BO、CO的中点，连结DE、EF、FG、OD．
1. （1）求证：四边形DEFG是平行四边形。
2. （2）若△ADE的面积为6，则四边形DEFG的面积为。
答案解析收藏纠错 + 选题
21. (2019九上·朝阳期中) 某商场以每件280元的价格购进一批商品，当每件商品售价为360元时，每月可售出60件，为了扩大销售，商场决定采取适当降价的方式促销，经调查发现，如果每件商品降价1元，那么商场每月就可以多售出5件。
1. （1）求降价前商场每月销售该商品的利润。
2. （2）如果使商场每月销售这种商品的利润达到7200元，且更有利于减少库存，求每件商品应降价的钱数。
答案解析收藏纠错 + 选题
22. (2019九上·朝阳期中) 在Rt△ABC中，∠ACB=90°，AB=5，AC=3．矩形DEFG的顶点D、G分别在边AC、BC上，EF在边AB上。
1. （1）点C到AB的距离为。
2. （2）如图①，若DE=DG，求矩形DEFG的周长。
3. （3）如图②，若矩形DEFG的周长是DE长的8倍，则矩形DEFG的周长为。
答案解析收藏纠错 + 选题

23. (2019九上·朝阳期中) 【教材呈现】下图是华师版九年级上册数学教材第38页的部分内容

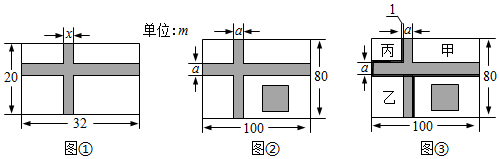
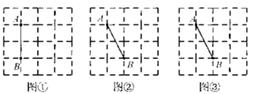
问题1：学校生物小组有一块长32m、宽20m的矩形试验田，为了管理方便，准备沿平行于两边的方向纵、橫各开辟一条等宽的小道．要使种植面积为540m² ，小道的宽应是多少?

分析：问题中没有明确小道在试验Ⅲ中的位置，试作出图①，不验发现小道的占地面积与位置无关。设小道宽为xm，则两条小道的面积分别为32xm²和20xm² ，其中重叠部分小方形的面积为x²m² ，根据题意，得…

（1）请根据教材提示，结合图①，写出完整的解题过程
（2）【结论应用】如图②，某小区附近有一块长100m，宽80m的长方形空地，在空地上有两条相同宽度的人行步道(纵·横)和个边长为人行步道宽度7倍的正方形休闲广场，两条人行步道的总面积与正方形休闲广场的面积相等，设人衍步道的宽为a(m)
求人行步道的宽。
（3）为了方便市民进行跑步健身，现按如图③所示方案增建塑胶跑道．知塑胶跑道的宽为1m，长方形区域甲的面积比长方形区域乙大441m² ，且区域丙为正方形，直接写出塑胶跑道的总面积。

答案解析收藏纠错 + 选题

24. (2019九上·朝阳期中) 如图，在△ABC中，∠ACB=90°，AB=10，AC=8，CD是边AB的中线．动点P从点C出发，以每秒5个单位长度的速度沿折线CD-DB向终点B运动．过点P作PQ⊥AC于点Q，以PQ为边作矩形PQMN，使点C、N始终在PQ的异侧，且PN= $\text{[math]}$ PQ，设矩形PQMN与△ACD重叠部分图形的面积是S，点P的运动时间为t（s）(t>0)。
1. （1）当点P在边CD上时，用含t的代数式表示PQ的长。
2. （2）当点N落在边AD上时，求t的值。
3. （3）求S与t之间的函数关系式
4. （4）连结DQ，当直线DQ将矩形PQMN分成面积比为1：2的两部分时、直接写出t的值。
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

吉林省长春市朝阳区2019-2020学年九年级上学期数学期中...

副标题：

*注意事项：

吉林省长春市朝阳区2019-2020学年九年级上学期数学期中...

试题分析

总体分析

题量分析

难度分析

知识点分析