![]()
 B .
B . 

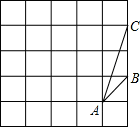
|
x |
… |
﹣1 |
﹣ | 0 | | 1 | | 2 | | 3 | … |
| y | … | m | | ﹣1 | | ﹣2 | | ﹣1 | | 2 | … |


|
x |
﹣2 |
﹣ | ﹣1 | ﹣ | | | 1 | 2 | 3 | 4 | … |
| y | 0 | ﹣ | ﹣1 | ﹣ | | | | m | | | … |
求m的值;