 B .
B .  C .
C .  D .
D . 
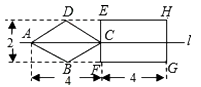
如图,直线l是菱形ABCD和矩形EFGH的对称轴,点C在EF边上,若菱形ABCD沿直线l从左向右匀速运动直至点C落在GH边上停止运动.能反映菱形进入矩形内部的周长y与运动的时间x之间关系的图象大致是( )
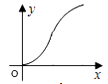 B .
B . 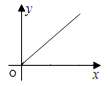 C .
C . 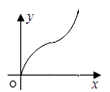 D .
D . 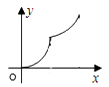
如图,将一副三角板按如图放置,则下列结论:①∠1=∠3;②如果∠2=30°,则有AC∥DE;③如果∠2=30°,则有BC∥AD;④如果∠2=30°,必有∠4=∠C.其中正确的有(只填序号);

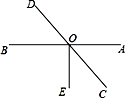
如图,AB、CD交于点O,∠AOE=90°,若∠AOC︰∠COE=5︰4,求∠AOD的度数.
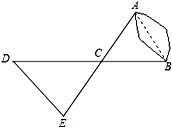
如图,A、B两点分别位于一个池塘的两侧,池塘西边有一座假山D,在DB的中点C处有一个雕塑,小川从点A出发,沿直线AC一直向前经过点C走到点E,并使CE=CA,然后他测量点E到假山D的距离,则DE的长度就是A、B两点之间的距离.
根据图2补全表格:

【阅读思考】
在数学思想中,有种解题技巧称之为“无中生有”.例如问题:将代数式 改成两个平方之差的形式.解:原式
﹒