陕西省宝鸡市凤翔县2019年九年级数学中考一模试卷

更新时间：2019-12-31 浏览次数：336 类型：中考模拟

一、单选题

1. (2024七下·惠城期中) $\text{[math]}$ 的算术平方根是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2021·阜宁模拟) 下列立体图形中，侧面展开图是扇形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2020七下·北海期末) 如图，直线l₁∥l₂ ，且分别与直线l交于C，D两点，把一块含30°角的三角尺按如图所示的位置摆放.若∠1=52°，则∠2的度数为（）

A . 92° B . 98° C . 102° D . 108°

答案解析收藏纠错 + 选题
4. (2019·凤翔模拟) 正比例函数y＝kx的图象如图所示，则k的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2019·凤翔模拟) 下列计算正确的是（）

A . x⁵+x⁵＝x⁵ B . x³ $\text{[math]}$ x³＝2x³ C . (﹣2x²)³＝8x⁸ D . x⁸÷x⁴＝x⁴

答案解析收藏纠错 + 选题
6. (2019·凤翔模拟) 如图，在△ABC中，AB＝2，BC＝4，△ABC的高AD与CE的比为（）

A . 1：2 B . 2：1 C . 1：4 D . 4：1

答案解析收藏纠错 + 选题
7. (2019·凤翔模拟) 已知一次函数y=kx﹣m﹣2x的图象与y轴的负半轴相交，且函数值y随自变量x的增大而减小，则下列结论正确的是（）

A . k＜2，m＞0 B . k＜2，m＜0 C . k＞2，m＞0 D . k＜0，m＜0

答案解析收藏纠错 + 选题
8. (2019·凤翔模拟) 如图，⨀O是△ABC的外接圆，直径AD＝4，∠ABC＝∠DAC，则AC的长为（　　）

A . 2 $\text{[math]}$ B . 2 C . 4 D . 6

答案解析收藏纠错 + 选题
9. (2019·凤翔模拟) 若二次函数y＝(k+1)x²﹣2 $\text{[math]}$ x+k的最高点在x轴上，则k的值为（）

A . 1 B . 2 C . ﹣1 D . ﹣2

答案解析收藏纠错 + 选题

二、填空题

10. (2019·凤翔模拟) 在实数1，﹣ $\text{[math]}$ ，0， $\text{[math]}$ 中，最大的数.

答案解析收藏纠错 + 选题
11. (2019八上·南昌期中) 如图，若正五边形和正六边形有一边重合，则∠BAC＝.

答案解析收藏纠错 + 选题
12. (2019·凤翔模拟) 已知A(x₁ ， y₁)，B(x₂ ， y₂)都在反比例函数y＝ $\text{[math]}$ 的图象上.若x₁x₂＝﹣4，则y₁ $\text{[math]}$ y₂的值为.

答案解析收藏纠错 + 选题
13. (2019·凤翔模拟) 如图，四边形ABCD，四边形EBFG，四边形HMPN均是正方形，点E、F、P、N分别在边AB、BC、CD、AD上，点H、G、M在AC上，阴影部分的面积依次记为S₁ ， S₂ ，则S₁：S₂等于.

答案解析收藏纠错 + 选题

三、解答题

14. (2020·陕西模拟) 计算： $\text{[math]}$ ×(﹣ $\text{[math]}$ )+|2﹣3 $\text{[math]}$ | $\text{[math]}$

答案解析收藏纠错 + 选题
15. (2019·凤翔模拟) 解方程： $\text{[math]}$ ﹣ $\text{[math]}$ ＝1

答案解析收藏纠错 + 选题
16. (2020·铜川模拟) 如图，已知△ABC，利用尺规在BC上找一点P，使得△ABP与△ACP均为直角三角形(不写作法，保留作图痕迹)

答案解析收藏纠错 + 选题
17. (2019·凤翔模拟) 如图，E、F分别是矩形ABCD的对角线AC和BD上的点，且AE=DF。求证：BE=CF

答案解析收藏纠错 + 选题

18. (2019·凤翔模拟) 中国飞人苏炳添以6秒47获得2019年国际田联伯明翰室内赛男子60米冠军，苏炳添夺冠掀起跑步热潮某校为了解该校八年级男生的短跑水平，全校八年级男生中随机抽取了部分男生，对他们的短跑水平进行测试，并将测试成绩(满分10分)绘制成如下不完整的统计图表：

组别	成绩/分	人数/人
A	5	36
B	6	32
C	7	15
D	8	8
E	9	5
F	10	m

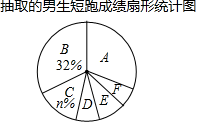
请你根据统计图表中的信息，解答下列问题：

（1）填空：m＝，n＝；
（2）所抽取的八年级男生短跑成绩的众数是分，扇形统计图中E组的扇形圆心角的度数为°；
（3）求所抽取的八年级男生短跑的平均成绩.

答案解析收藏纠错 + 选题

19. (2019·凤翔模拟) 汉江是长江最长的支流，在历史上占居重要地位，陕西省境内的汉江为汉江上游段.李琳利用热气球探测器测量汉江某段河宽，如图，探测器在A处观测到正前方汉江两岸岸边的B、C两点，并测得B、C两点的俯角分别为45°，30°已知A处离地面的高度为80m，河平面BC与地面在同一水平面上，请你求出汉江该段河宽BC.(结果保留根号)

答案解析收藏纠错 + 选题
20. (2021八下·庐江期末) 快递公司为提高快递分拣的速度，决定购买机器人来代替人工分拣，两种型号的机器人的工作效率和价格如表：

型号

甲

乙

每台每小时分拣快递件数(件)

1000

800

每台价格(万元)

5

3

该公司计划购买这两种型号的机器人共10台，并且使这10台机器人每小时分拣快递件数总和不少于8500件
1. （1）设购买甲种型号的机器人x台，购买这10台机器人所花的费用为y万元，求y与x之间的关系式；
2. （2）购买几台甲种型号的机器人，能使购买这10台机器人所花总费用最少？最少费用是多少？
答案解析收藏纠错 + 选题
21. (2020·铜川模拟) 西安市历史文化底蕴深厚，旅游资源丰富，钟楼、大雁塔兵马俑三个景点是人们节假日游玩的热门景点
1. （1）李辉从这三个景点中随机选取一个景点去游玩，求他去钟楼的概率；
2. （2）张慧、王丽两名同学，各自从三个景点中随机选取一个作为周末游玩的景点，用树状图或列表法求他们同时选中大雁塔的概率.
答案解析收藏纠错 + 选题
22. (2019·凤翔模拟) 如图，AB是⨀O的直径，点C在⨀O上，AD和过C点的切线互相垂直，垂足为D
1. （1）求证：AC平分∠DAB；
2. （2）若点M是AB的中点，CM交AB于点N，求证：BM²＝MC•MN.
答案解析收藏纠错 + 选题
23. (2019·凤翔模拟) 如图，已知抛物线C₁：y＝﹣x²+4，将抛物线C1沿x轴翻折，得到抛物线C₂
1. （1）求出抛物线C₂的函数表达式；
2. （2）现将抛物线C₁向左平移m个单位长度，平移后得到的新抛物线的顶点为M，与x轴的交点从左到右依次为A，B；将抛物线C₂向右也平移m个单位长度，平移后得到的新抛物线的顶点为N，与x轴交点从左到右依次为D，E.在平移过程中，是否存在以点A，N，E，M为顶点的四边形是矩形的情形？若存在，请求出此时m的值；若不存在，请说明理由.
答案解析收藏纠错 + 选题
24. (2019·凤翔模拟) (1)如图1，A、B是⨀O上的两个点，点P在⨀O上，且△APB是直角三角形，⨀O的半径为1
1. （1） ①请在图1中画出点P的位置.
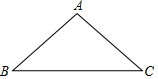
  ②当AB＝1时，∠APB＝°.
2. （2）如图2，⨀O的半径为5，A、B为⨀O外固定两点(O、A、B三点不在同一直线上)，且OA＝9，P为⊙O上的一个动点(点P不在直线AB上)，以PA和AB为作平行四边形PABC，求BC的最小值，并确定此时点P的位置；
3. （3）如图3，A、B是⊙O上的两个点，过A点作射线AM⊥AB，AM交⨀O于点C，若AB＝3，AC＝4，点D是平面内的一个动点，且CD＝2，E为BD的中点，在D的运动过程中，求线段AE长度的最大值与最小值.
答案解析收藏纠错 + 选题