陕西省铜川市新区2020年数学中考一模试卷

更新时间：2020-09-28 浏览次数：307 类型：中考模拟

一、选择题

1. (2020·铜川模拟) 计算：（﹣ $\text{[math]}$ ）²﹣1=（）

A . ﹣ $\text{[math]}$ B . ﹣ $\text{[math]}$ C . ﹣ $\text{[math]}$ D . 0

答案解析收藏纠错 + 选题
2. (2021·北部湾模拟) 如图，将直角三角形绕其一条直角边所在直线l旋转一周，得到的几何体是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2024八上·重庆市期末) 如图，∠B＝40°，∠ACD＝108°，若B，C，D三点在一条直线上，则∠A的大小是（　　）

A . 148° B . 78° C . 68° D . 50°

答案解析收藏纠错 + 选题
4. (2020·铜川模拟) 对于正比例函数y＝﹣3x，当自变量x的值增加1时，函数y的值增加（　　）

A . ﹣3 B . 3 C . ﹣ $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2020·铜川模拟) 计算（-2x²y）³的结果是（）

A . -8x⁶y³ B . 6x⁶y³ C . -8x⁵y³ D . -6x⁵y³

答案解析收藏纠错 + 选题
6. (2020·铜川模拟) 如图，在△ABC中，∠BAC=90°， AB=20， AC=15， △ABC的高AD与角平分线CF交于点E，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023八下·石家庄期中) 如图，已知直线l₁：y=﹣2x+4与直线l₂：y=kx+b（k≠0）在第一象限交于点M．若直线l₂与x轴的交点为A（﹣2，0），则k的取值范围是（）

A . ﹣2＜k＜2 B . ﹣2＜k＜0 C . 0＜k＜4 D . 0＜k＜2

答案解析收藏纠错 + 选题
8. (2020·铜川模拟) 如图，在矩形ABCD中，E为AD的中点，∠BED的平分线EF交BC于点F，若AB=6，BC=16，则FC的长度为（　　）

A . 4 B . 5 C . 6 D . 8

答案解析收藏纠错 + 选题
9. (2020·铜川模拟) 如图，已知⊙O的半径为5，弦AB，CD所对的圆心角分别是∠AOB，COD，若∠AOB与∠COD互补，弦CD=6，则弦AB的长为（）

A . 6 B . 8 C . 5 $\text{[math]}$ D . 5 $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023九上·武汉月考) 已知二次函数 $\text{[math]}$ ( $\text{[math]}$ 为常数)，当自变量 $\text{[math]}$ 的值满足 $\text{[math]}$ 时，与其对应的函数值 $\text{[math]}$ 的最大值为-1，则 $\text{[math]}$ 的值为（）

A . 3或6 B . 1或6 C . 1或3 D . 4或6

答案解析收藏纠错 + 选题

二、填空题

11. (2020·铜川模拟) 分解因式：x³﹣2x²+x= ．

答案解析收藏纠错 + 选题
12. (2020·铜川模拟) 如图，在五边形ABCDE中，∠A+∠B+∠E＝300°，DP、CP分别平分∠EDC、∠BCD，则∠CPD的度数是.

答案解析收藏纠错 + 选题
13. (2020九上·永定期中) 如图，平面直角坐标系中，等腰 $\text{[math]}$ 的顶点 $\text{[math]}$ 分别在 $\text{[math]}$ 轴、 $\text{[math]}$ 轴的正半轴， $\text{[math]}$ $\text{[math]}$ 轴，点 $\text{[math]}$ 在函数 $\text{[math]}$ 的图象上.若 $\text{[math]}$ 则 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
14. (2020·铜川模拟) 如图，已知正方形ABCD中，AB＝6，E是边AD的中点，P是边CD上的动点，Q是半圆BC上的动点，则PE+PQ的最小值是.

答案解析收藏纠错 + 选题

三、解答题

15. (2020·铜川模拟) 计算： $\text{[math]}$ +（π﹣5）⁰﹣|2 $\text{[math]}$ ﹣3|.

答案解析收藏纠错 + 选题
16. (2021八下·南山期末) 解分式方程： $\text{[math]}$ + $\text{[math]}$ ＝1．

答案解析收藏纠错 + 选题
17. (2020·铜川模拟) 如图，已知△ABC，利用尺规在BC上找一点P，使得△ABP与△ACP均为直角三角形(不写作法，保留作图痕迹)

答案解析收藏纠错 + 选题
18. (2024·湖北模拟) 如图，在矩形ABCD中，E是AB的中点，连接DE、CE.

求证：△ADE≌△BCE.

答案解析收藏纠错 + 选题
19. (2020·铜川模拟) 家访是学校与家庭沟通的有效渠道，是形成教育合力的关键，是转化后进生的催化剂.某市教育局组织全市中小学教师开展家访活动活动过程中，教育局随机抽取了部分教师调查其近两周家访次数，将采集到的数据按家访次数分成五类，并分别绘制了下面的两幅不完整的统计图.

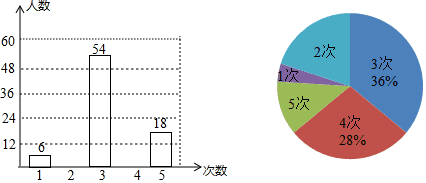
请根据以上信息，解答下列问题：
1. （1）请把条形统计图补充完整；
2. （2）所抽取的教师中，近两周家访次数的众数是次，平均每位教师家访次；
3. （3）若该市有12000名教师，请估计近两周家访不少于3次的教师有多少名？
答案解析收藏纠错 + 选题
20. (2020·铜川模拟) 如图，小华和小康想用标杆来测量河对岸的树AB的高，两人在确保无安全隐患的情况下，小康在F处竖立了一根标杆EF，小华走到C处时，站立在C处看到标杆顶端E和树的顶端B在一条直线上，此时测得小华的眼睛到地面的距离DC＝16米；然后，小华在C处蹲下，小康平移标杆到H处时，小华恰好看到标杆顶端G和树的顶端B在一条直线上，此时测得小华的眼睛到地面的距离MC＝0.8米.已知EF＝GH＝2.4米，CF＝2米，FH＝1.6米，点C、F、H、A在一条直线上，点M在CD上，CD⊥AC，EF⊥AC，CH⊥AC，AB⊥AC，根据以上测量过程及测量数据，请你求出树AB的高度.

答案解析收藏纠错 + 选题

21. (2020·铜川模拟) 油炸冰激凌是以面包、鸡蛋、冰激凌为材料制作的一种西式小吃，某油炸冰激凌专卖店每天固定制作甲、乙两个款型的油炸冰激凌共1000个，且所有产品当天全部售出，原料成本、销售单价及店员生产提成如表所示：

	甲（元/个）	乙（元/个）
原料成本	10	8
销售单价	20	16
生产提成	2	1.5

设该店每天制作甲款型的油炸冰激凌x个，每天获得的总利润为y元

（1）求出y与x之间的函数关系式；
（2）若该店每天投入总成本不超过10750元，应怎样安排甲、乙两种款型的制作量，可使该店这一天所获得的利润最大？并求出最大利润（总成本＝原料成本+生产提成，利润＝销售收入﹣投入总成本）

答案解析收藏纠错 + 选题

22. (2020·铜川模拟) 某翻译团为成为2022年冬奥会志愿者做准备，该翻译团一共有五名翻译，其中一名只会翻译西班牙语，三名只会翻译英语，还有一名两种语言都会翻译.
1. （1）求从这五名翻译中随机挑选一名会翻译英语的概率；
2. （2）若从这五名翻译中随机挑选两名组成一组，请用树状图或列表的方法求该纽能够翻译上述两种语言的概率.
答案解析收藏纠错 + 选题
23. (2020·铜川模拟) 如图，已知AB是⊙O的直径，AC，BC是⊙O的弦，OE∥AC交BC于E，过点B作⊙O的切线交OE的延长线于点D，连接DC并延长交BA的延长线于点F.
1. （1）求证：DC是⊙O的切线；
2. （2）若∠ABC＝30°，AB＝8，求线段CF的长.
答案解析收藏纠错 + 选题
24. (2020·铜川模拟) 已知抛物线L：y＝x²+bx+c经过点M（2，﹣3），与y轴交于点C（0，﹣3）.
1. （1）求抛物线L的表达式；
2. （2）试判断抛物线L与x轴交点的情况；
3. （3）平移该抛物线，设平移后的抛物线为L′，抛物线L′的顶点记为P，它的对称轴与x轴交于点Q，已知点N（2，﹣8），怎样平移才能使得以M、N、P、Q为顶点的四边形为菱形？
答案解析收藏纠错 + 选题
25. (2020·铜川模拟)
1. （1）问题提出：
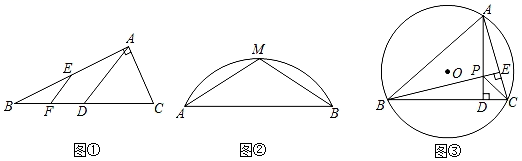
  如图①，在Rt△BAC中，∠BAC＝90°，点D，E分别是CB，AB的中点，点F是BD的中点，若AB＝8，AC＝6，则EF＝；
2. （2）问题探究：
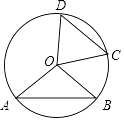
  如图②，已知：M是弓形AB上的中点，AB＝24，弓形AB的高是8，则对应⊙O的面积为多少？（结果保留根号或π）
3. （3）问题解决：
  如图③，在半径为5的⊙O中，弦BC＝8，点A为优弧BC上的动点，过点A作AD⊥BC于点D，过点B作BE⊥AC于点E.AD和BE交于点P，连接PC，试求△PBC面积的最大值.
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

陕西省铜川市新区2020年数学中考一模试卷

副标题：

*注意事项：

陕西省铜川市新区2020年数学中考一模试卷

试题分析

总体分析

题量分析

难度分析

知识点分析