一、选择题(本大题共12小题,每小题3分,满分36分。在每个小题给出的四个选项中,只有一项是正确的,每小题选对得3分,选错、不选或多选均得0分。)
-
-
-
A . 2x+1=0
B . x2+3x+5=0
C . y2+x=1
D .  +x2+1=0
+x2+1=0
-
A . 51°
B . 56°
C . 68°
D . 78°
-
A . 4cm
B . 6cm
C . 8cm
D . 10cm
-
A . x=0
B . x=2
C . x=0或x=2
D . x=0或x=-2
-
A . 有两个不相等的实数根
B . 有两个相等的实数根
C . 只有一个实数根
D . 没有实数根
-
A . 开口向上
B . 对称轴是直线x=1
C . 顶点坐标是(-1,3)
D . 函数y有最小值
-
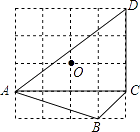
9.
(2020七上·滦南期末)
如图,点A、B、C、D、O都在方格纸的格点上,若△COD是由△AOB绕点O按逆时针方向旋转而得,则旋转的角度为( )
A . 30°
B . 45°
C . 90°
D . 135°
-
A . x<-1
B . x>3
C . -1<x<3
D . x>3或x<-1
-
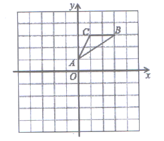
A . △ACD的外心
B . △ABC的外心
C . △ACD的内心
D . △ABC的内心
-
12.
(2019九上·柳江月考)
如图,一条抛物线与x轴相交于M,N两点(点M在点N的左侧),其顶点P在线段AB上移动,点A,B的坐标分别为(-2,-3),(1,-3),点N的横坐标的最大值为4,则点M的横坐标的最小值为( )

A . -1
B . -3
C . -5
D . -7
二、填空题(本大题共6小题,每小题3分,满分18分.请将答案直接填写在答题卡中相应的横线上,在草稿纸、试卷上答题无效)
-
-
-
-
-
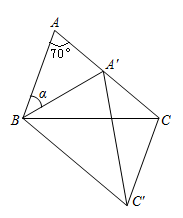
17.
(2019九上·柳江月考)
如图,在△ABC中,∠A=70°,AC=BC,以点B为旋转中心把△ABC顺时针旋转a度,得到△A'BC',点A'恰好落在AC上,则∠ACC'=
。
-
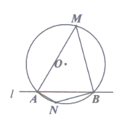
18.
(2019九上·柳江月考)
如图,⊙O的半径是2,直线1与⊙O相交于A、B两点,M,N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB的面积最大值是
。
三、解答题(本大题共8小题,满分66分.解答时应写出必要的文字说明、演算步骤或推理过程请将解答写在答题卡中相应的区域内,画图或作辅助线时使用铅笔画出,确定后必须使用黑色字迹时签字笔描黑在草稿纸、试卷上答题无效)
-
-
-
-
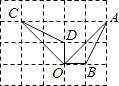
(1)
①画出△ABC关于点O的中心对称图形△A
1B
1C
1;
②画出△ABC绕原点O逆时针旋转90°△A2B2C2 , 写出点C2的坐标。
-
(2)
若△ABC上任意一点P(m,n)绕原点O逆时针旋转90°的对应点为Q,则点Q的坐标为。(用含m,n的式子表示)
-
-
23.
(2020九上·扬州月考)
习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气”。某校为响应我市全民阅读活动,利用节假日面向社会开放学校图书馆。据统计,第一个月进馆500人次,进馆人次逐月增加,第三个月进馆720人次,若进馆人次的月平均增长率相同。
-
-
(2)
因条件限制,学校图书馆每月接纳能力不超过1000人次,在进馆人次的月平均增长率不变的条件下,校图书馆能否接纳第四个月的进馆人次,并说明理由。
-
-
(1)
求证:

,
-
-
25.
(2019九上·柳江月考)
如图,已知AB是⊙O的直径,点C是AB延长线上的一点,点D在⊙O上且AD=CD,∠C=30°。

-
-
(2)
若⊙O的半径为5,求

的长。
-
26.
(2020九上·广东期末)
如图所示,已知二次函数y=-x
2+bx+c的图像与x轴的交点为点A(3,0)和点B,与y轴交于点C(0,3),连接AC。

-
-
(2)
在(1)中位于第一象限内的抛物线上是否存在点D,使得△ACD的面积最大?若存在,求出点D的坐标及△ACD面积的最大值,若不存在,请说明理由。
-
(3)
在抛物线上是否存在点E,使得△ACE是以AC为直角边的直角三角形如果存在,请直接写出点E的坐标即可;如果不存在,请说明理由。

 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D .