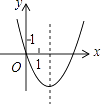 B .
B . 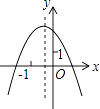 C .
C . 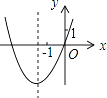 D .
D . 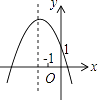
| x | … | 0 | | 4 | … |
| y | … | 0.37 | -1 | 0.37 | … |
则方程ax2+bx+1.37=0的根是( )
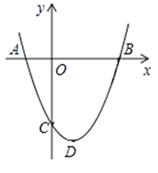

①如图2,当n< AC时,求证:△PAM≌△NCP;
②直接用含n的代数式表示线段PQ的长;
③若PM的长为 ,当二次函数
的图象经过平移同时过点P和点N时,请直接写出此时的二次函数表达式.