 B .
B .  C .
C . 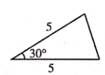 D .
D . 
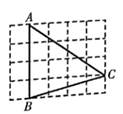

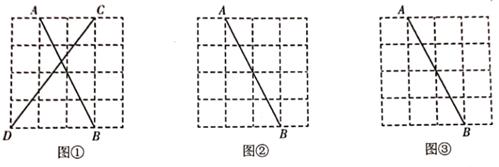
要求:所画线段CD的位置不同,点C、D均在格点上。
【参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90】
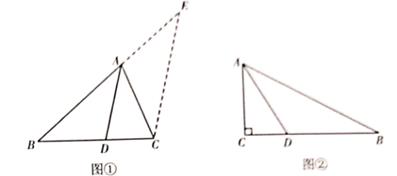
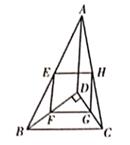
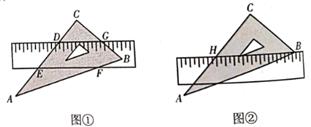
如图①,在△ABC中,AD平分∠BAC交BC于点D,则 。
提示:过点C作CE∥AD交BA的延长线于点E。
请根据上面的提示,写出得到“ “这一结论完整的证明过程。
结论应用:如图②2,在Rt△ABC中,∠C=90°,AC=8,BC=15,AD平分∠BAC交BC于点D。请直接利用“问题探究”的结论,求线段CD的长。