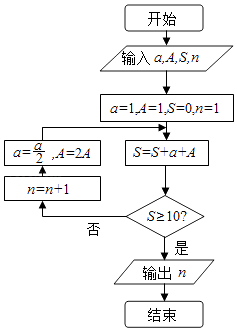
 B .
B .  C .
C .  D .
D . 
(Ⅰ)求角B的值;
(Ⅱ)若b= ≤a,求2a﹣c的取值范围.

(Ⅰ)指出这组数据的众数和中位数;
(Ⅱ)若视力测试结果不低丁5.0,则称为“好视力”,求校医从这16人中随机选取3人,至多有1人是“好视力”的概率;
(Ⅲ)以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记ξ表示抽到“好视力”学生的人数,求ξ的分布列及数学期望.
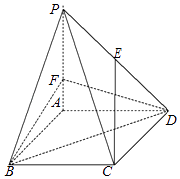
(Ⅰ)若 AF=1,求证:CE∥平面 BDF;
(Ⅱ)若 AF=2,求平面 BDF 与平面 PCD所成的锐二面角的余弦值.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)当 ⊥
=0时,求△OPQ面积的最大值.
(Ⅰ)记 ,讨论函数F(x)的单调性;
(Ⅱ)令G(x)=af(x)+g(x)(a∈R),若函数G(x)有两个零点,求实数a的取值范围.