初中数学浙教版八年级下册第三章数据分析初步章末检测

更新时间：2020-02-20 浏览次数：352 类型：单元试卷

一、单选题

1. 某公司欲招聘一名工作人员，对甲应聘者进行面试和笔试，面试成绩为85分，笔试成绩为90分若公司分别赋予面试成绩和笔试成绩7和3的权，则下列算式表示甲的平均成绩的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. 某班学生军训射击，有m人各打中a环，n人各打中b环，那么该班打中a环和b环学生的平均环数是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2019九上·桂林期末) 为了解某班学生每天的睡眠情况，随机选择该班5名学生进行调查．在一段时间里，平均每人每天的睡眠时间统计如下(单位：小时)：6，8，8，7，9．由此估计该班学生平均每人每天的睡眠时间为（）

A . 7小时 B . 7.5小时 C . 7.6小时 D . 8小时

答案解析收藏纠错 + 选题
4. (2019七下·桂平期末) 若一组数据2，3，x，5，7的众数为7，则这组数据的中位数为（）

A . 2 B . 3 C . 5 D . 7

答案解析收藏纠错 + 选题
5. (2019九下·揭西期中) 2018年某中学举行的春季田径径运动会上，参加男子跳高的15名运动员的成绩如表所示：这些运动员跳高成绩的中位数和众数分别是（）

A . 1.70 $\text{[math]}$ ，1.65 $\text{[math]}$ B . 1.70 $\text{[math]}$ ，1.70 $\text{[math]}$ C . 1.65 $\text{[math]}$ ，1.60 $\text{[math]}$ D . 3 $\text{[math]}$ ，4 $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2019八下·余杭期中) 一组数据1，2，3，4，4，10．去掉10，剩下的数据原数据相比，不变的是（）

A . 平均数 B . 中位数 C . 众数 D . 平均数和众数

答案解析收藏纠错 + 选题
7. (2020·尧都模拟) 图1，图2分别是某厂六台机床十月份第一天和第二天生产零件数的统计图，与第一天相比，第二天六台机床生产零件数的平均数与方差的变化情况是（）

A . 平均数变大，方差不变 B . 平均数变小，方差不变 C . 平均数不变，方差变小 D . 平均数不变，方差变大

答案解析收藏纠错 + 选题

8. 甲、乙两名运动员进行射击练习，每人射击5次，成绩（单位：环）如下表所示：下列说法错误的是（）

	第1次	第2次	第3次	第4次	第5次	平均成绩
甲	7	▲	8	10	8	8
乙	7	8	8	9	8	▲

A . 甲运动员的第2次射击成绩为7环 B . 乙运动员的平均射击成绩为8环 C . 甲运动员这5次射击成绩的方差为6 D . 乙运动员的成绩更稳定

答案解析收藏纠错 + 选题

9. (2023八下·金东月考) 若一组数据x₁＋1，x₂＋1，…，x_n＋1的平均数为17，方差为2，则另一组数据x₁＋2，x₂＋2，…，x_n＋2的平均数和方差分别为（）

A . 17，2 B . 18，2 C . 17，3 D . 18，3

答案解析收藏纠错 + 选题
10. (2019八下·如皋期中) 某专卖店专营某品牌的衬衫，店主对上一周中不同尺码的衬衫销售情况统计如下：

尺码

39

40

41

42

43

平均每天销售数量/件

6

15

21

12

9

该店主决定本周进货时，增加了一些41码的衬衫，影响该店主决策的统计量是（）

A . 平均数 B . 中位数 C . 方差 D . 众数

答案解析收藏纠错 + 选题

二、填空题

11. 8个数的平均数12，4个数的平均为18，则这12个数的平均数为.

答案解析收藏纠错 + 选题
12. 一组数据a，b，c，d，e的平均数是7，则另一组数据a+2，b+2，c+2，d+2，e+2的平均数为.

答案解析收藏纠错 + 选题
13. (2021八下·诸暨期中) 一组数据1、3、4、5、x、9的众数和中位数相同，那么x的值是

答案解析收藏纠错 + 选题
14. (2024八下·潘集期末) “植树节”时，九(1)班6个小组的植树棵数分别是：5，7，3，x，6，4.已知这组数据的众数是5，则该组数据的平均数是

答案解析收藏纠错 + 选题
15. 已知一组数据0，1，2，2，x，3的平均数是2，则这组数据的方差是．

答案解析收藏纠错 + 选题
16. (2018八上·兰州期末) 已知一组数据a、b、c、d. e方差为3，则另一组数据a+3，b+3，c+3，d+3，e+3的方差为，

答案解析收藏纠错 + 选题

三、综合题

17. (2019七上·包河期中) 七（1）班共45名学生，在一次数学测试中以90分为标准，超过的记为正，不足的记为负，成绩如下：

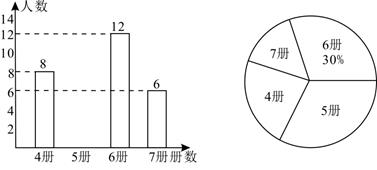
人数

5

10

8

12

4

5

1

成绩

-1

+3

-2

+1

+10

0

-4

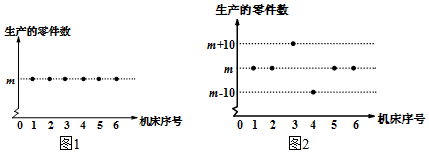
请你算出这次考试的平均成绩（精确到0.1分）

答案解析收藏纠错 + 选题
18. (2019八下·马山期末) 某校八年级学生某科目期末评价成绩是由完成作业、单元检测、期末考试三项成绩构成的，如果期末评价成绩80分以上（含80分），则评为“优秀”．下面表中是小张和小王两位同学的成绩记录：

完成作业

单元测试

期末考试

小张

70

90

80

小王

60

75
1. （1）若按三项成绩的平均分记为期末评价成绩，请计算小张的期末评价成绩；
2. （2）若按完成作业、单元检测、期末考试三项成绩按的权重来确定期末评价成绩．
  ①请计算小张的期末评价成绩为多少分？
  
  ②小王在期末（期末成绩为整数）应该最少考多少分才能达到优秀？
答案解析收藏纠错 + 选题

19. (2018八上·沈河期末) 某校八年级甲、乙两班分别选5名同学参加“学雷锋读书活动”演讲比赛，其预赛成绩如图：

（1）根据上图求出下表所缺数据；

	平均数	中位数	众数	方差
甲班	8.5	8.5
乙班		8	10	1.6

（2）根据上表中的平均数、中位数和方差你认为哪班的成绩较好？并说明你的理由.

答案解析收藏纠错 + 选题

20. 王老师为了了解学生在数学学习中常见错误的纠正情况，收集整理了学生在作业和考试中的常见错误，编制了10道选择题，每题3分，对他所教的八年（1）班和八年（2）班进行了检测．如图所示表示从两班随机抽取的10名学生的得分情况：

（1）利用图中提供的信息，补全如表：

班级	平均分（分）	中位数（分）	众数（分）
八年（1）班		24	24
八年（2）班	24

（2）你认为那个班的学生纠错的得分情况比较整齐一些，通过计算说明理由．

答案解析收藏纠错 + 选题

21. (2018·秦淮模拟) 如图，甲、乙两人在一次射击比赛中击中靶的情况（击中靶中心“×”所在的圆面为10环，靶中各数字表示该数所在圆环被击中所得的环数），每人射击了6次．
1. （1）请用列表法将他俩的射击成绩统计出来；
2. （2）请你运用所学的统计知识做出分析，从两个不同角度评价甲、乙两人的打靶成绩．
答案解析收藏纠错 + 选题

22. (2019八下·长兴期末) 某公司招聘职员两名，对甲、乙、丙、丁四名候选人进行了笔试和面试，各项成绩满分均为100分，然后再按笔试占60%，面试占40%计算候选人的综合成绩(满分为100分)

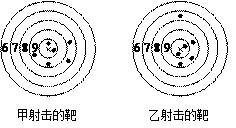
他们的各项成绩如下表所示：

候选人	笔试成绩/分	面试成绩/分
甲	90	88
乙	84	92
丙	x	90
丁	88	86

（1）这四名候选人面试成绩的中位数是。
（2）现得知候选人丙的综合成绩为87.6分，则表中x的值等于。
（3）求其余三名候选人的综合成绩，并以综合成绩排序确定所要招聘的前两名的人选。

答案解析收藏纠错 + 选题

23. 省射击队为从甲、乙两名运动员中选拔一人参加全国比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：

	第一次	第二次	第三次	第四次	第五次	第六次
甲	10	8	9	8	10	9
乙	10	7	10	10	9	8

（1）根据表格中的数据，计算出甲的平均成绩是环，乙的平均成绩是环；
（2）分别计算甲、乙六次测试成绩的方差；
（3）根据（1）、（2）计算的结果，你认为推荐谁参加全国比赛更合适，请说明理由．

答案解析收藏纠错 + 选题

24. (2021八下·樊城期末) 高尔基说：“书，是人类进步的阶梯.”阅读可以丰富知识、拓展视野、充实生活等诸多益处.为了解学生的课外阅读情况，某校随机抽查了部分学生阅读课外书册数的情况，并绘制出如下统计图.其中条形统计图因为破损丢失了阅读5册书数的数据.
1. （1）求条形图中丢失的数据，并写出阅读书册数的众数和中位数；
2. （2）根据随机抽查的这个结果，请估计该校1200名学生中课外阅读5册书的学生人数；
3. （3）若学校又补查了部分同学的课外阅读情况，得知这部分同学中课外阅读最少的是6册，将补查的情况与之前的数据合并后发现中位数并没有改变，试求最多补查了多少人？
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中