3.141， ，
，
，0，
，0.1010010001
B . 
C . 
D . 
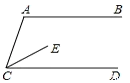
如图，将一副三角板和一张对边平行的纸条按下列方式摆放，两个三角板的一直角边重合，含30°角的直角三角板的斜边与纸条一边重合，含45°角的三角板的一个顶点在纸条的另一边上，则∠1的度数是．
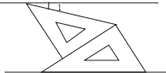
求证： DG∥BA．
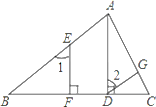
证明：∵AD⊥BC，EF⊥BC ( 已知 )
∴∠EFB=90°，∠ADB=90°( )
∴∠EFB=∠ADB ( 等量代换 )
∴EF∥AD ( )
∴∠1=∠BAD ()
又∵∠1=∠2 ( 已知)
∴ （等量代换）
∴DG∥BA． ()
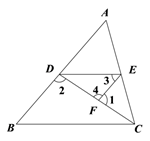
证明：∵∠1+∠4＝180°（平角定义）
∠1+∠2＝180°（已知）
∴（）
∴∥（）
∴∠3+∠=180°（）
又∵∠3=∠B（已知）
∴∠ +∠=180°（等量代换）
∴∥（）
∴∠AED＝∠ACB（）．
位于点， 
位于点；
与 的距离是，与 
的距离是；
三角形中一边中点与这边所对顶点的线段称为三角形的中线．
三角形的中线的性质：三角形的中线等分三角形的面积．
即如图，AD是 中BC边上的中线，则
，
理由： ，
，
即：等底同高的三角形面积相等．
操作与探索：
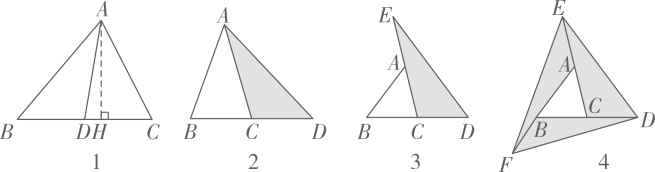
在如图至如图中， 的面积为a．
如图，已知四边形ABCD的面积是a；E，F，G，H分别是AB，BC，CD的中点，求图中阴影部分的面积？
位于点（3，0）上，则
