一百馒头一百僧,大僧三个更无争,
小僧三人分一个,大小和尚得几丁.
意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人,下列求解结果正确是( )

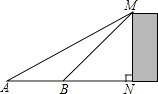
如图,为了测量某建筑物MN的高度,在平地上A处测得建筑物顶端M的仰角为30°,向N点方向前进16m到达B处,在B处测得建筑物顶端M的仰角为45°,则建筑物MN的高度等于( )
 B .
B .  C .
C . 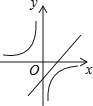 D .
D . 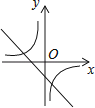
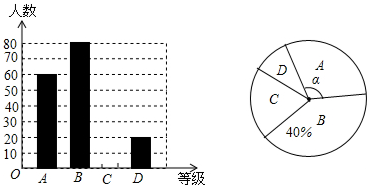
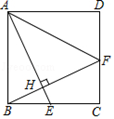
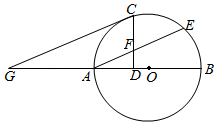
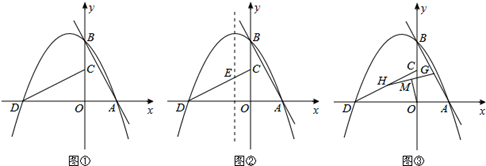
如图,已知抛物线y= x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
