备考2020年中考数学二轮复习拔高训练卷专题5 函数的实际...

更新时间：2020-03-20 浏览次数：622 类型：二轮复习

一、单选题

1. (2023九上·双峰期中) 三角形的面积为12cm² ，这时底边上的高ycm底边xcm之间的函数关系用图象表示大致是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2017九上·深圳期中) 某小学部课外兴趣小组的同学每人制作一个面积为1m²的矩形学具进行展示。设矩形的宽为x米，长为y米。那么这些同学所制作的矩形长y（m）与宽x（m）之间的函数关系的图象大致是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. 某体育场计划修建一个容积一定的长方体游泳池，设容积为a（m³），泳池的底面积S（m²）与其深度x（m）之间的函数关系式为S= $\text{[math]}$ （x＞0），该函数的图象大致是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
4. 某品牌钢笔进价8元，按10元1支出售时每天能卖出20支，市场调查发现如果每支每涨价1元，每天就少卖出2支，为了每天获得最大利润，其售价应定为（）

A . 11元 B . 12元 C . 13元 D . 14元

答案解析收藏纠错 + 选题
5.
已知一块蓄电池的电压为定值，以此蓄电池为电源时，电流I（A）与电阻R（Ω）之间的函数关系如图，如果以此蓄电池为电源的用电器限制电流不超过10A，那么此用电器的可变电阻为（　　）

A . 不小于3.2Ω B . 不大于3.2Ω C . 不小于12Ω D . 不大于12Ω

答案解析收藏纠错 + 选题
6. 山东全省2016年国庆假期旅游人数增长12.5%，其中尤其是乡村旅游最为火爆．泰山脚下的某旅游村，为接待游客住宿需要，开设了有100张床位的旅馆，当每张床位每天收费100元时，床位可全部租出，若每张床位每天收费提高20元，则相应的减少了10张床位租出，如果每张床位每天以20元为单位提高收费，为使租出的床位少且租金高，那么每张床位每天最合适的收费是（）

A . 140元 B . 150元 C . 160元 D . 180元

答案解析收藏纠错 + 选题
7.
在一个可以改变体积的密闭容器内装有一定质量的二氧化碳，当改变容器的体积时，气体的密度也会随之改变，密度ρ（单位：kg/m³）是体积V（单位：m³）的反比例函数，它的图象如图所示，当V=10m³时，气体的密度是（　　）

A . 5kg/m³ B . 2kg/m³ C . 100kg/m³ D . 1kg/m³

答案解析收藏纠错 + 选题
8. (2021八下·曲阳期末)
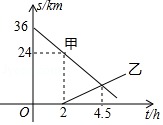
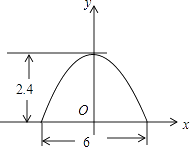
如图是本地区一种产品30天的销售图象，图①是产品日销售量y（单位：件）与时间t（单位；天）的函数关系，图②是一件产品的销售利润z（单位：元）与时间t（单位：天）的函数关系，已知日销售利润=日销售量×一件产品的销售利润，下列结论错误的是（　　）

A . 第24天的销售量为200件 B . 第10天销售一件产品的利润是15元 C . 第12天与第30天这两天的日销售利润相等 D . 第30天的日销售利润是750元

答案解析收藏纠错 + 选题
9. 竖直向上发射的小球的高度h（m）关于运动时间t（s）的函数表达式为h=at²+bt，其图象如图所示，若小球在发射后第2秒与第6秒时的高度相等，则下列时刻中小球的高度最高的是（）

A . 第3秒 B . 第3.9秒 C . 第4.5秒 D . 第6.5秒

答案解析收藏纠错 + 选题
10.
如图，市煤气公司计划在地下修建一个容积为10⁴m³的圆柱形煤气储存室，则储存室的底面积S（单位：m²）与其深度d（单位：m）的函数图象大致是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
11. 如图，隧道的截面是抛物线，可以用y= $\text{[math]}$ 表示，该隧道内设双行道，限高为3m，那么每条行道宽是（）

A . 不大于4m B . 恰好4m C . 不小于4m D . 大于4m，小于8m

答案解析收藏纠错 + 选题
12. 某种产品按质量分为10个档次，生产最低档次产品，每件获利润8元，每提高一个档次，每件产品利润增加2元．用同样工时，最低档次产品每天可生产60件，提高一个档次将减少3件．如果获利润最大的产品是第k档次（最低档次为第一档次，档次依次随质量增加），那么k等于（　　）

A . 5 B . 7 C . 9 D . 10

答案解析收藏纠错 + 选题

二、填空题

13. (2021·吉水模拟) 甲、乙两人分别从A，B两地相向而行，他们距B地的距离s（km）与时间t（h）的关系如图所示，那么乙的速度是km/h．

答案解析收藏纠错 + 选题
14. (2018·青岛模拟) 甲、乙两动点分别从线段AB的两端点同时出发，甲从点A出发，向终点B运动，乙从点B出发，向终点A运动．已知线段AB长为90cm，甲的速度为2.5cm/s．设运动时间为x（s），甲、乙两点之间的距离为y（cm），y与x的函数图象如图所示，则图中线段DE所表示的函数关系式为．（并写出自变量取值范围）

答案解析收藏纠错 + 选题
15. (2020九上·梁子湖期中) 某菜农搭建了一个横截面为抛物线的大棚，尺寸如图，若菜农身高为1.8m，他在不弯腰的情况下，在棚内的横向活动范围是 m．

答案解析收藏纠错 + 选题
16. (2016九上·武清期中) 一位运动员投掷铅球，如果铅球运行时离地面的高度为y（米）关于水平距离x（米）的函数解析式为y=﹣ $\text{[math]}$ ，那么铅球运动过程中最高点离地面的距离为米．

答案解析收藏纠错 + 选题
17. 某商店经销一种成本为每千克40元的水产品，据市场分析，若按每千克50元销售，一个月能售出500千克，若销售价每涨1元，则月销售量减少10千克．要使月销售利润达到最大，销售单价应定为元．

答案解析收藏纠错 + 选题
18.
某公园草坪的防护栏形状是抛物线形．为了牢固起见，每段护栏按0.4m的间距加装不锈钢的支柱，防护栏的最高点距底部0.5m（如图），则其中防护栏支柱A₂B₂的长度为 m．

答案解析收藏纠错 + 选题

三、解答题

19. (2019·泰州) 小李经营一家水果店，某日到水果批发市场批发一种水果．经了解，一次性批发这种水果不得少于 $\text{[math]}$ ，超过 $\text{[math]}$ 时，所有这种水果的批发单价均为3元 $\text{[math]}$ ．图中折线表示批发单价 $\text{[math]}$ （元 $\text{[math]}$ ）与质量 $\text{[math]}$ 的函数关系．
1. （1）求图中线段 $\text{[math]}$ 所在直线的函数表达式；
2. （2）小李用800元一次可以批发这种水果的质量是多少？
答案解析收藏纠错 + 选题
20. (2022九上·上思期中) 某工厂设计了一款产品，成本为每件20元．投放市场进行试销，经调查发现，该种产品每天的销售量y（件）与销售单价x（元）之间满足y=﹣2x+80 （20≤x≤40），设销售这种产品每天的利润为W（元）．
（1）求销售这种产品每天的利润W（元）与销售单价x（元）之间的函数表达式；
（2）当销售单价定为多少元时，每天的利润最大？最大利润是多少元？

答案解析收藏纠错 + 选题
21. (2019九上·天津期中) 由于雾霾天气趋于严重，我市某电器商城根据民众健康需求，代理销售某种家用空气净化器，其进价是200元/台．经过市场销售后发现：在一个月内，当售价是400元/台时，可售出200台，且售价每降低10元，就可多售出50台．若供货商规定这种空气净化器售价不能低于300元/台，代理销售商每月要完成不低于450台的销售任务．
1. （1）完成下列表格，并直接写出月销售量y（台）与售价x（元/台）之间的函数关系式及售价x的取值范围；
  
  售价（元/台）
  
  月销售量（台）
  
  400
  
  200
  
  ▲
  
  250
  
  x
  
  ▲
2. （2）当售价x（元/台）定为多少时，商场每月销售这种空气净化器所获得的利润w（元）最大？最大利润是多少？
答案解析收藏纠错 + 选题
22. (2018九下·游仙模拟) 绵阳某工厂从美国进口A、B两种产品销售，已知每台A种产品进价为3000元，售价为4800元；受中美贸易大战的影响，每台B种产品的进价上涨500元，进口相同数量的B种产品，在中美贸易大战开始之前只需要60万元，中美贸易大战开始之后需要80万元。
1. （1）中美贸易大战开始之后，每台B种产品的进价为多少？
2. （2）中美贸易大战开始之后，如果A种产品的进价和售价不变，每台B种产品在进价的基础上提高40%作为售价。公司筹集到不多于35万元且不少于33万元的资金用于进口A、B两种产品共150台，请你设计一种进货方案使销售后的总利润最大。
答案解析收藏纠错 + 选题
23. (2019九上·秀洲期中) 某商场要经营一种新上市的文具，进价为20元 $\text{[math]}$ 件．试营销阶段发现：当销售单价是25元时，每天的销售量为150件；销售单价每上涨1元，每天的销售量就减少10件．设销售单价为 $\text{[math]}$ （元 $\text{[math]}$ ，每天的销售量为 $\text{[math]}$ （件 $\text{[math]}$ ，每天所得的销售利润 $\text{[math]}$ （元 $\text{[math]}$ ．
1. （1）求出 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数关系式；
2. （2）求出 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数关系式，并求当销售单价为多少元时，该文具每天的销售利润最大，最大利润为多少？
答案解析收藏纠错 + 选题
24. (2018九上·彝良期末) 某商品的进价为每件40元，售价为每件50元，每个月可卖出210件；如果每件商品的售价每上涨1元，则每个月少卖10件(每件售价不能高于65元)．设每件商品的售价上x元(x为正整数)，每个月的销售利润为y元．
1. （1）求y与x的函数关系式并直接写出自变量戈的取值范围；
2. （2）每件商品的售价定为多少元时，每个月可获得最大利润?最大的月利润是多少元?
3. （3）每件商品的售价定为多少元时，每个月的利润恰为2200元?
答案解析收藏纠错 + 选题
25. (2019·广西模拟) 某市化工材料经销公司购进一种化工原料若干千克，价格为每千克30元．物价部门规定其销售单价不高于每千克60元，不低于每千克30元．经市场调查发现：日销售量y(千克)是销售单价x(元)的一次函数，且当x=60时，y=80；x=50时，y=100．在销售过程中，每天还要支付其他费用450元．
1. （1）求出y与x的函数关系式，并写出自变量龙的取值范围；
2. （2）求该公司销售该原料日获利W(元)与销售单价x(元)之间的函数关系式；
3. （3）当销售单价为多少元时，该公司日获利最大?最大获利是多少元?
答案解析收藏纠错 + 选题