吉林省长春市净月高新区2019年中考数学模拟考试试卷

更新时间：2021-05-20 浏览次数：319 类型：中考模拟

一、单选题

1. (2024九下·金山模拟) $\text{[math]}$ 的相反数是（）

A . $\text{[math]}$ B . 2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2019·高新模拟) 今年清明小长假期问，长春净月某景区接待游客约为51700人次，数字51700用科学记数法表示为（　　）

A . 51.7×10³ B . 5.17×10⁴ C . 5.17×10⁵ D . 0.517×10⁵

答案解析收藏纠错 + 选题
3. (2022·李沧模拟) 如图所示的正六棱柱的主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2019·高新模拟) 不等式3x﹣3≤0解集在数轴上表示正确是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2021·延边州模拟) 如图，AE∥DB，∠1＝85°，∠2＝28°，则∠C的度数为（　　）

A . 55° B . 56° C . 57° D . 60°

答案解析收藏纠错 + 选题
6. (2019·高新模拟) 如图，要测量河两相对的两点P、A之间的距离，可以在AP的垂线PB上取点C，测得PC＝100米，用测角仪测得∠ACP＝40°，则AP的长为（　　）

A . 100sin40°米 B . 100tan40°米 C . $\text{[math]}$ 米 D . $\text{[math]}$ 米

答案解析收藏纠错 + 选题
7. (2020·永年模拟) 如图，O为圆心， $\text{[math]}$ 是直径， $\text{[math]}$ 是半圆上的点， $\text{[math]}$ 是 $\text{[math]}$ 上的点.若 $\text{[math]}$ ，则 $\text{[math]}$ 的大小为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2019·高新模拟) 如图，在平面直角坐标系中，Rt△ABC的顶点A、B的坐标分别为（﹣1，1）、（3，0），直角顶点C在x轴上，在△ADE中，∠E＝90°，点D在第三象限的双曲线y＝ $\text{[math]}$ 上，且边AE经过点C．若AB＝AD，∠BAD＝90°，则k的值为（　　）

A . 3 B . 4 C . ﹣6 D . 6

答案解析收藏纠错 + 选题

二、填空题

9. (2019八上·哈尔滨期中) 分解因式： $\text{[math]}$ =．

答案解析收藏纠错 + 选题
10. (2019·高新模拟) 一元二次方程2x²﹣4x+1＝0实数根（填“有”或“无”）

答案解析收藏纠错 + 选题
11. (2019·高新模拟) 我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有八十足．问鸡兔各几何？”若设鸡有x只，兔有y只，请将题中数量关系用二元一次方程组列出得．

答案解析收藏纠错 + 选题
12. (2020·开封模拟) 如图，在△ABC中，∠ACB=90°.按以下步骤作图，分别以点A和点B为圆心，大于 $\text{[math]}$ 的长为半径作圆弧，两弧交于点E和点F；作直线EF交AB于点D；连结CD，若AC=8，BC=6，则CD的长为.

答案解析收藏纠错 + 选题
13. (2019·高新模拟) 如图，已知双曲线 $\text{[math]}$ （k＜0）经过直角三角形OAB斜边OA的中点D，且与直角边AB相交于点C．若点A的坐标为（﹣6，4），则△AOC的面积为．

答案解析收藏纠错 + 选题
14. (2019·高新模拟) 在平面直角坐标系中，将二次函数y＝﹣x²+x+6在x轴上方的图象沿x轴翻折到x轴下方，图象的其余部分不变，将这个新函数的图象记为G（如图所示）．当直线y＝m与图象G有4个交点时，则m的取值范围是．

答案解析收藏纠错 + 选题

三、解答题

15. (2019·高新模拟) 先化简，再求值：（ $\text{[math]}$ ﹣1）÷ $\text{[math]}$ ，其中x＝2

答案解析收藏纠错 + 选题
16. (2019·高新模拟) 某校期末评选出四名“优秀课代表”，其中有2名男生和2名女生，若从他们中任选2人作为代表发言，请用画树状图（或列表）的方法，求恰好选中1男1女的概率．

答案解析收藏纠错 + 选题
17. (2022八上·株洲期中) 用A、B两种机器人搬运大米，A型机器人比B型机器人每小时多搬运20袋大米，A型机器人搬运700袋大米与B型机器人搬运500袋大米所用时间相等．求A、B型机器人每小时分别搬运多少袋大米．

答案解析收藏纠错 + 选题
18. (2019·高新模拟) 如图，在菱形ABCD中，对角线AC与BD交于点O．过点C作BD的平行线，过点D作AC的平行线，两直线相交于点E．
1. （1）求证：四边形OCED是矩形；
2. （2）若CE＝2，DE＝3，求菱形ABCD的面积．
答案解析收藏纠错 + 选题
19. (2019·高新模拟) 如图，线段AB经过圆心O，交⊙O于点A、C，点D为⊙O上一点，连结AD、OD、BD，∠A＝∠B＝30°．
1. （1）求证：BD是⊙O的切线．
2. （2）若OA＝5，求OA、OD与AD围成的扇形的面积．
答案解析收藏纠错 + 选题

20. (2019·高新模拟) 某校学生会为了解本校学生每天体育锻炼所用时间情况，采用问卷的方式对一部分学生进行调查确定调查对象时，大家提出以下几种方案：（A）对各班体育委员进行调査；（B）对某班的全体学生进行调查；（C）从全校每班随机抽5名学生进行调查在问卷调查时，每位被调查的学都选择了问卷中适合自己的十个时间段，学生会将收集到的数据整理后续制成如下的统计表：

被调查的学生每天体育锻炼所用时间统计表

组别	时间x（小时）	频数
一	0≤x≤0.5	15
二	0.6＜x≤1	27
三	1＜x≤1.5	38
四	1.5＜x≤2	13
五	x＞2	7

（1）为了使收集到的数据具有代表性，学生会在确定调查对象时选择了方案（填A、B或C）；
（2）被调查的学生每天体育锻炼所用时间的中位数落在组；
（3）根据以上统计结果，估计该校900名学生中每天体育锻炼时间不超过0.5小时的人数，并根据你计算的结果提出一条合理化建议．

答案解析收藏纠错 + 选题

21. (2019·高新模拟) 一辆轿车从甲地驶往乙地，到达乙地后立即返回甲地，速度是原来的1.5倍，往返共用t小时.一辆货车同时从甲地驶往乙地，到达乙地后停止.两车同时出发，匀速行驶，设轿车行驶的时间为x（h），两车离开甲地的距离为y（km），两车行驶过程中y与x之间的函数图象如图所示.
1. （1）轿车从乙地返回甲地的速度为km/t，t=h ；
2. （2）求轿车从乙地返回甲地时y与x之间的函数关系式；
3. （3）当轿车从甲地返回乙地的途中与货车相遇时，求相遇处到甲地的距离.
答案解析收藏纠错 + 选题
22. (2019·高新模拟) 图①、图②、图③均为方形网格，每个小正方形的顶点称为格点，每个小正方形的边长均为1．

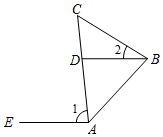
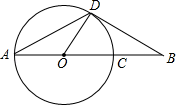
（探究）在图①中，点A、B、C、D均为格点．证明：BD平分∠ABC．

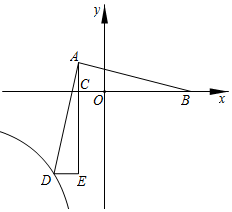
（应用）在图②、图③中，点M、O、N均为格点．
1. （1）利用（探究）的方法，在图②、图③中分别找到一个格点P，使OP平分∠MON．要求：图②、图③中所画的图形不相同，保留画图痕迹．
2. （2） cos∠MOP的值为．
答案解析收藏纠错 + 选题
23. (2019·高新模拟) 如图，在矩形ABCD中，AB＝6 $\text{[math]}$ ，BC＝3 $\text{[math]}$ 动点P从点A出发，沿AC以每秒4个单位长度的速度向终点C运动．过点P（不与点A、C重合）作EF⊥AC，交AB或BC于点E，交AD或DC于点F，以EF为边向右作正方形EFGH设点P的运动时间为t秒．
1. （1） ①AC＝．②当点F在AD上时，用含t的代数式直接表示线段PF的长．
2. （2）当点F与点D重合时，求t的值．
3. （3）设方形EFGH的周长为l，求l与t之间的函数关系式．
4. （4）直接写出对角线AC所在的直线将正方形EFGH分成两部分图形的面积比为1：2时t的值．
答案解析收藏纠错 + 选题
24. (2020·长春模拟) 在平面直角坐标系中，对于点P（x，y）和Q（x，y′），给出如下定义：如果y′＝ $\text{[math]}$ ，那么称点Q为点P的“伴随点”．

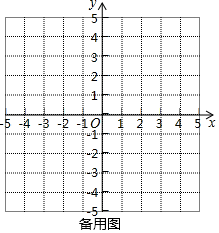
例如：点（5，6）的“伴随点”为点（5，6）；点（﹣5，6）的“伴随点”为点（﹣5，﹣6）．
1. （1）直接写出点A（2，1）的“伴随点”A′的坐标．
2. （2）点B（m，m+1）在函数y＝kx+3的图象上，若其“伴随点”B′的纵坐标为2，求函数y＝kx+3的解析式．
3. （3）点C、D在函数y＝﹣x²+4的图象上，且点C、D关于y轴对称，点D的“伴随点”为D′．若点C在第一象限，且CD＝DD′，求此时“伴随点”D′的横坐标．
4. （4）点E在函数y＝﹣x²+n（﹣1≤x≤2）的图象上，若其“伴随点”E′的纵坐标y′的最大值为m（1≤m≤3），直接写出实数n的取值范围．
答案解析收藏纠错 + 选题