 B .
B . 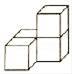 C .
C . 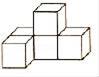 D .
D . 
 B .
B .  C .
C .  D .
D . 

20 | 21 | 19 | 16 | 27 | 18 | 31 | 29 | 21 | 22 |
25 | 20 | 19 | 22 | 35 | 33 | 19 | 17 | 18 | 29 |
18 | 35 | 22 | 15 | 18 | 18 | 31 | 31 | 19 | 22 |
整理上面数据,得到条形统计图:

样本数据的平均数、众数、中位数如下表所示:
统计量 | 平均数 | 众数 | 中位数 |
数值 | 23 | m | 21 |
根据以上信息,解答下列问题:
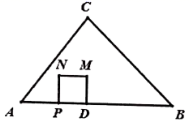
要求:借助网格,只用无刻度的直尺,不要求写出画法.

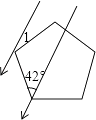
已知:如图, ,垂足为点
,
,点
是直线
上的任意一点.
求证: .

分析:图中的两个直角三角形 和
,只要证明这两个三角形全等,便可证明
(请写出完整的证明过程)
求证:直线 、
、
交于点.
例如:点(5,6)的“伴随点”为点(5,6);点(﹣5,6)的“伴随点”为点(﹣5,﹣6).