B . 
C . 
D . 
B . 
C . 
D . 
B . 
C . 
D . 
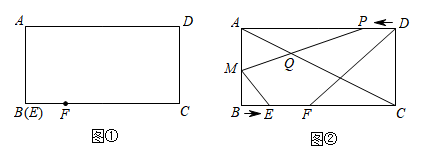
如图，将一条长度为1的线段三等分，然后取走其中的一份，称为第一次操作；再将余下的每一条线段三等分，然后取走其中一份，称为第二次操作；…如此重复操作，当第n次操作结束时，被取走的所有线段长度之和为 ．
甲厂：76，74，74，76，73，76，76，77，78，74，76，70，76，76，73，70，77，79，78，71；
甲厂鸡腿质量频数统计表
| 质量 | 频数 | 频率 |
| | 2 | 0.1 |
| | 3 | 0.15 |
| | 10 | |
| | 5 | 0.25 |
| 合计 | 20 | 1 |
乙厂：75，76，77，77，78，77，76，71，74，75，79，71，72，74，73，74，70，79，75，77；
乙厂鸡腿质量频数分布直方图
分析上述数据，得到下表：
| 统计量 厂家 | 平均数 | 中位数 | 众数 | 方差 |
| 甲厂 | 75 | 76 | | 6.3 |
| 乙厂 | 75 | 75 | 77 | 6.6 |
请你根据图表中的信息完成下列问题：
【问题提出】求的值（其中
是正整数）．
【问题解决】为解决上述问题，我们借鉴已有的经验，采用由特殊到一般，归纳的研究方法，利用数形结合法，借助图形进行推理获得结论．
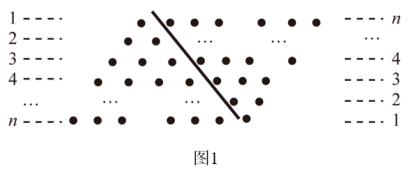
探究1：如图2，可以看成1个
的正方形的面积，即
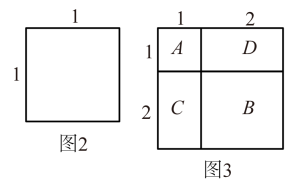
探究2：如图3，表示1个
的正方形，其面积为：
；
表示1个
的正方形，其面积为：
；
分别表示1个
的长方形，其面积的和为：
；
的面积和为
， 而
恰好可以拼成一个
的大正方形．由此可得：
．
例如：棱长是1的正方体有：个，
棱长是2的正方体有：个，
……
棱长是6的正方体有：个；
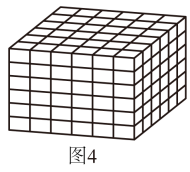
然后利用上面归纳的结论，通过计算，可得图4中大小正方体的个数为．
观察下列各式：
若（
为正整数）按上面规律展开后，发现等式右边含有“2021”这个数，则
的值．
