河南省信阳市罗山县2016-2017学年八年级下学期数学期末...

更新时间：2017-09-04 浏览次数：736 类型：期末考试

一、选择题

1. (2017八下·厦门期中) 下列二次根式中，不能与 $\text{[math]}$ 合并的是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. 下列运算正确的是（）

A . $\text{[math]}$ + $\text{[math]}$ = $\text{[math]}$ B . 2 $\text{[math]}$ × $\text{[math]}$ =6 $\text{[math]}$ C . $\text{[math]}$ = $\text{[math]}$ D . 5 $\text{[math]}$ ﹣2 $\text{[math]}$ =3 $\text{[math]}$

答案解析收藏纠错 + 选题
3. 某校在体育健康测试中，有8名男生“引体向上”的成绩（单位：次）分别是：14，12，10，8，9，16，12，7，这组数据的中位数和众数分别是（）

A . 10，12 B . 12，11 C . 11，12 D . 12，12

答案解析收藏纠错 + 选题
4. 某中学随机地调查了50名学生，了解他们一周在校的体育锻炼时间，结果如下表所示：
时间（小时）
5
6
7
8
人数
10
15
20
5
则这50名学生这一周在校的平均体育锻炼时间是（　　）

A . 6.2小时 B . 6.4小时 C . 6.5小时 D . 7小时

答案解析收藏纠错 + 选题
5. 如图，在给定的一张平行四边形纸片上作一个菱形．甲、乙两人的作法如下：
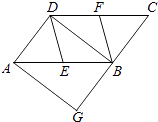
甲：连接AC，作AC的垂直平分线MN分别交AD，AC，BC于M，O，N，连接AN，CM，则四边形ANCM是菱形．
乙：分别作∠A，∠B的平分线AE，BF，分别交BC，AD于E，F，连接EF，则四边形ABEF是菱形．
根据两人的作法可判断（）

A . 甲正确，乙错误 B . 乙正确，甲错误 C . 甲、乙均正确 D . 甲、乙均错误

答案解析收藏纠错 + 选题
6. 小张的爷爷每天坚持锻炼身体，星期天爷爷从家里跑步到公园，打了一会儿太极拳，然后沿原路漫步走到家，下面能反映当天爷爷离家的距离y（米）与时间x（分钟）之间关系的大致图象的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. 如图．在Rt△ABC中，∠ABC=90°，点D是斜边上的中点，点P在AB上，PE⊥BD于E，PF⊥AC于F，若AB=6，BC=3，则PE+PF=（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. 如图，在Rt△ABC中，∠B=90°，AB=3，BC=4，点D在BC上，以AC为对角线的所有▱ADCE中，DE最小的值是（）

A . 2 B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题
9. 现有一只蜗牛和一只乌龟从同一点分别沿正东和正南方向爬行，蜗牛的速度为14厘米/分钟，乌龟的速度为48厘米/分钟，5分钟后，蜗牛和乌龟的直线距离为（　　）

A . 300厘米 B . 250厘米 C . 200厘米 D . 150厘米

答案解析收藏纠错 + 选题
10. (2016七下·沂源开学考) 勾股定理是几何中的一个重要定理．在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载．如图1是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理．图2是由图1放入矩形内得到的，∠BAC=90°，AB=3，AC=4，点D，E，F，G，H，I都在矩形KLMJ的边上，则矩形KLMJ的面积为（）

A . 90 B . 100 C . 110 D . 121

答案解析收藏纠错 + 选题

二、填空题

11. (2017八下·武清期中) 计算： $\text{[math]}$ =．

答案解析收藏纠错 + 选题
12. 若一次函数y=（a+3）x+a﹣3不经过第二象限，则a的取值范围是．

答案解析收藏纠错 + 选题
13. 如图，直线y₁=kx+b经过点A（﹣1，﹣2）和点B（﹣2，0），直线y₂=2x经过点A，当y₁＜y₂时，x的取值范围是．

答案解析收藏纠错 + 选题
14. 甲、乙两班举行电脑汉字输入比赛，参赛学生每分钟输入汉字的个数经统计计算后填入下表：
班级
参赛人数
平均字数
中位数
方差
甲
55
135
149
191
乙
55
135
151
110
某同学根据上表分析得出如下结论：①甲、乙两班学生成绩的平均水平相同；②乙班优秀人数多于甲班优秀人数（每分钟输入汉字数≥150个为优秀）；③甲班的成绩波动比乙班的成绩波动大，上述结论正确的是．

答案解析收藏纠错 + 选题
15. 如图1，正方形纸片ABCD的边长为2，翻折∠B、∠D，使两个直角的顶点重合于对角线BD上一点P，EF、GH分别是折痕（如图2）．设AE=x（0＜x＜2），给出下列判断：
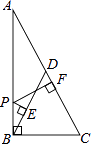
①当x=1时，点P是正方形ABCD的中心；
②当x= $\text{[math]}$ 时，EF+GH＞AC；
③当0＜x＜2时，六边形AEFCHG面积的最大值是 $\text{[math]}$ ；
④当0＜x＜2时，六边形AEFCHG周长的值不变．
其中正确的是（写出所有正确判断的序号）．

答案解析收藏纠错 + 选题

三、解答题

16. 计算：
1. （1）（ $\text{[math]}$ ﹣ $\text{[math]}$ ）﹣（ $\text{[math]}$ +2 $\text{[math]}$ ）；
2. （2）（2 $\text{[math]}$ ﹣ $\text{[math]}$ ）²+（ $\text{[math]}$ + $\text{[math]}$ ） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
17. 罗山县尚文学校组织了一次环保知识竞赛，每班选25名同学参加比赛，成绩分为A，B，C，D四个等级，其中相应等级的得分依次记为100分、90分、80分、79分，学校将某年级的一班和二班的成绩整理并绘制成如下的统计图：请根据以上提供的信息解答下列问题：
1. （1）
  把一班竞赛成绩统计图补充完整：
2. （2）填表：
  
  平均数（分）
  中位数（分）
  众数（分）
  一班
  90
  二班
  87.6
  80
3. （3）请从以下给出的三个方面中任选一个对这次竞赛成绩的结果进行分析；①从平均数和中位数方面来比较一班和二班的成绩；②从平均数和众数方面来比较一班和二班的成绩；③从B级以上（包括B级）的人数方面来比较一班和二班的成绩．
答案解析收藏纠错 + 选题
18. 如图，直线l经过点A（1，6）和点B（﹣3，﹣2）．
1. （1）求直线l的解析式，直线与坐标轴的交点坐标；
2. （2）求△AOB的面积．
答案解析收藏纠错 + 选题
19. 嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的，她先用尺规作出了如图1的四边形ABCD，并写出了如下不完整的已知和求证．
1. （1）已知：如图1，在四边形ABCD中，BC=AD，AB=
  求证：四边形ABCD是四边形．
  填空，补全已知和求证；
2. （2）按嘉淇的想法写出证明；
3. （3）用文字叙述所证命题的逆命题为．
答案解析收藏纠错 + 选题
20. 甲、乙两人匀速从同一地点到1500米处的图书馆看书，甲出发5分钟后，乙以50米/分的速度沿同一路线行走．设甲、乙两人相距s（米），甲行走的时间为t（分），s关于t的函数图象的一部分如图所示．
1. （1）求甲行走的速度；
2. （2）在坐标系中，补画s关于t的函数图象的其余部分；
3. （3）问甲、乙两人何时相距360米？
答案解析收藏纠错 + 选题
21. (2017八下·罗平期末) 如图，在▱ABCD中，E、F分别为边AB、CD的中点，BD是对角线，过点A作AG∥DB交CB的延长线于点G．
1. （1）求证：DE∥BF；
2. （2）若∠G=90°，求证：四边形DEBF是菱形．
答案解析收藏纠错 + 选题
22. 如图1是甲、乙两个圆柱形水槽的轴截面示意图，乙槽中有一圆柱形铁块立放其中（圆柱形铁块的下底面完全落在乙槽底面上），现将甲槽中的水匀速注入乙槽．甲、乙两个水槽中水的深度y（cm）与注水时间x（分）之间的关系如图2所示．根据图象解答下列问题：
1. （1）图2中折线ABC表示槽中水的深度与注水时间之间的关系．线段DE表示槽中水的深度与注水时间之间的关系．点B的纵坐标的实际意义是．
2. （2）注水多长时间，甲、乙两个水槽中水的深度相同．
3. （3）若乙槽底面积为36cm² ，（壁厚不计），求乙槽中铁块的体积．
4. （4）若乙槽中铁块的体积为112cm³ ，则甲槽的底面积是cm² ．
答案解析收藏纠错 + 选题
23.
提出问题：如图1，将三角板放在正方形ABCD上，使三角板的直角顶点P在对角线AC上，一条直角边经过点B，另一条直角边交边DC与点E，求证：PB=PE
分析问题：学生甲：如图1，过点P作PM⊥BC，PN⊥CD，垂足分别为M，N通过证明两三角形全等，进而证明两条线段相等．
学生乙：连接DP，如图2，很容易证明PD=PB，然后再通过“等角对等边”证明PE=PD，就可以证明PB=PE了．
解决问题：请你选择上述一种方法给予证明．
问题延伸：如图3，移动三角板，使三角板的直角顶点P在对角线AC上，一条直角边经过点B，另一条直角边交DC的延长线于点E，PB=PE还成立吗？若成立，请证明；若不成立，请说明理由．

答案解析收藏纠错 + 选题