福建省漳州市云霄县2019年中考数学一模考试试卷

更新时间：2024-07-13 浏览次数：206 类型：中考模拟

一、选择题（共10小题，每小题4分，满分40分.每小题只有一个正确的选项，请把正确的选项填涂在答题卡的相应位置）

1. (2019·云霄模拟) 2019的相反数是（）

A . 2019 B . ﹣2019 C . $\text{[math]}$ D . ﹣ $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2021·盘锦)
图中三视图对应的正三棱柱是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2019·云霄模拟) 下列运算正确的是（）

A . （﹣a）³＝a³ B . （a²）³＝a⁵ C . a²÷a^﹣2＝1 D . （﹣2a³）²＝4a⁶

答案解析收藏纠错 + 选题
4. (2019·云霄模拟) 2018年5月21日，西昌卫星发射中心成功发射探月工程嫦娥四号任务“鹊桥号”中继星，卫星进入近地点高度为200公里、远地点高度为40万公里的预定轨道．将数据40万用科学记数法表示为（）

A . 4×10⁴ B . 4×10⁵ C . 4×10⁶ D . 0.4×10⁶

答案解析收藏纠错 + 选题
5. (2023七下·宝安期中) 如图，直线a∥b ，点B在直线b上，且AB⊥BC ， ∠1＝55°，那么∠2的度数是（）

A . 20° B . 30° C . 35° D . 50°

答案解析收藏纠错 + 选题
6. (2021七下·滁州期末) 不等式组 $\text{[math]}$ 的解集在数轴上表示正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2021七下·渠县期末) 如图，在方格纸中，以AB为一边作△ABP ，使之与△ABC全等，从P₁ ， P₂ ， P₃ ， P₄四个点中找出符合条件的点P的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 1

答案解析收藏纠错 + 选题
8. (2019·云霄模拟) 1275年我国南宋数学家杨辉提出一个问题：直田积（矩形面积）八百六十四步（平方步），只云阔（宽）不及长一十二步（宽比长少一十二步），问阔及长各几步．设阔（宽）为x步，则所列方程正确的是（）

A . x（x+12）＝864 B . x（x﹣12）＝864 C . （x﹣12）（x+12）＝864 D . 12x＝864

答案解析收藏纠错 + 选题
9. (2019·云霄模拟) 如图，已知直线y＝ $\text{[math]}$ x﹣3与x轴、y轴分别交于A、B两点，P是以C（0，1）为圆心，1为半径的圆上一动点，连结PA、PB ．则△PAB面积的最大值是（）

A . 8 B . 12 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2021九上·衡阳期末) 如图，抛物线y＝ax²+bx+c（a≠0）的对称轴为直线x＝1，与x轴的一个交点坐标为A（3，0），其部分图象如图所示，下列结论中：①b²＜4ac；②方程ax²+bx+c＝0的两个根是x₁＝﹣1，x₂＝3；③2a+b＝0；④a+b+c＜0；⑤当0＜x＜3时，y随x增大而减小；其中结论正确的个数是（）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题

二、填空题（共6小题，每小题4分，满分24分.）

11. (2019·云霄模拟) 计算：（﹣2）⁰﹣ $\text{[math]}$ ＝．

答案解析收藏纠错 + 选题
12. (2019·云霄模拟) 如图，测量试管口径的量具ABC ， AB的长为4.5cm ， AC被分为60等份．如果试管口DE正好对着量具上20等份处（DE∥AB），那么试管口径DE是cm ．

答案解析收藏纠错 + 选题
13. (2019·云霄模拟) 两组数据m，6，n与1，m，2n，7的平均数都是6，若将这两组数据合并成一组数据，则这组新数据的中位数为．

答案解析收藏纠错 + 选题
14. (2019·云霄模拟) 如图，AB为半圆的直径，且AB＝4，半圆绕点B顺时针旋转36°，点A旋转到A'的位置，则图中阴影部分的面积为（结果保留π）．

答案解析收藏纠错 + 选题
15. (2019·云霄模拟) 对于任意实数t ，抛物线y＝x²+（2﹣t）x+t总经过一个固定的点P ，若反比例函数 $\text{[math]}$ 经过点P ，则k＝．

答案解析收藏纠错 + 选题
16. (2019·云霄模拟) 如图，△ABC∽△ADE ， ∠BAC＝∠DAE＝90°，AB＝8，AC＝6，F是DE的中点，若点E是直线BC上的动点，连接BF ，则BF的最小值是．

答案解析收藏纠错 + 选题

三、解答题（共9题，满分86分.）

17. (2019·云霄模拟) 先化简，再求值： $\text{[math]}$ ，其中x＝sin45°．

答案解析收藏纠错 + 选题
18. (2019·云霄模拟) 已知：如图，∠BAC＝∠DAM ， AB＝AN ， ∠B＝∠ANM ，求证：AD＝AM ．

答案解析收藏纠错 + 选题
19. (2019·云霄模拟) 如图，已知∠ABC ，求作：▱ABCD（要求：①尺规作图，保留作图痕迹，不写作法；②用两种方法作图）

答案解析收藏纠错 + 选题
20. (2019·云霄模拟) 如图，已知△ABC内接于⊙O ， AD为直径，点C在劣弧AB上（不与点A ， B重合），设∠DAB＝α，∠ACB＝β，小明同学通过画图和测量得到以下近似数据：

α

30°

35°

40°

50°

60°

80°

β

120°

125°

130°

140°

150°

170°

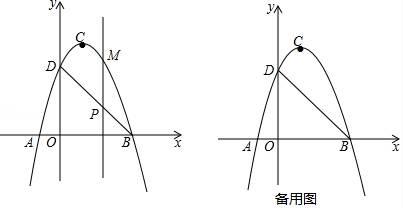
猜想：α关于β的函数表达式，并给出证明．

答案解析收藏纠错 + 选题
21. (2019·云霄模拟) “校园诗歌大赛”结束后，张老师和李老师将所有参赛选手的比赛成绩（得分均为整数）进行整理，并分别绘制成扇形统计图和频数直方图．部分信息如下：
1. （1）本次比赛参赛选手共有人，扇形统计图中“69.5～79.5”这一组人数占总参赛人数的百分比为；
2. （2）赛前规定，成绩由高到低前40%的参赛选手获奖．某参赛选手的比赛成绩为82分，试判断他能否获奖，并说明理由；
3. （3）成绩前四名是2名男生和2名女生，若从他们中任选2人作为获奖代表发言，试求恰好选中1男1女的概率．
答案解析收藏纠错 + 选题
22. (2019·云霄模拟) 如图，用48米篱笆围成一个外形为矩形的花园，花园一面利用院墙，中间用一道篱笆间隔成两个小矩形，院墙的长度为20米，平行于院墙的一边长为x米，花园的面积为S平方米．
1. （1）求S与x之间的函数关系式；
2. （2）问花园面积可以达到180平方米吗？如果能，花园的长和宽各是多少？如果不能，请说明理由．
答案解析收藏纠错 + 选题
23. (2019·云霄模拟) 已知点P（m ， n）和直线y＝kx+b ，则点P到直线y＝kx+b的距离可用公式d＝ $\text{[math]}$ 计算．
例如：求点P（﹣1，2）到直线y＝3x+7的距离．

解：因为直线y＝3x+7，其中k＝3，b＝7．

所以点P（﹣1，2）到直线y＝3x+7的距离为d＝ $\text{[math]}$ ．

根据以上材料，解答下列问题：
1. （1）直接写出点P（1，1）到直线y＝﹣2x+4的距离d＝；
2. （2）已知直线y＝﹣2x+4与y＝﹣2x﹣5平行，求这两条直线之间的距离．
3. （3）已知⊙Q的圆心Q坐标为（0，5），半径r为2，判断⊙Q与直线 $\text{[math]}$ 的位置关系并说明理由．
答案解析收藏纠错 + 选题
24. (2019·云霄模拟) 【问题情境】
1. （1）古希腊著名数学家欧几里得在《几何原本》提出了射影定理，又称“欧几里德定理”：在直角三角形中，斜边上的高是两条直角边在斜边射影的比例中项，每一条直角边又是这条直角边在斜边上的射影和斜边的比例中项．射影定理是数学图形计算的重要定理．
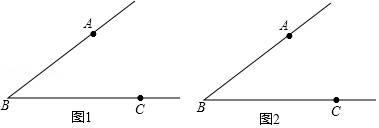
  其符号语言是：如图1，在Rt△ABC中，∠ACB＝90°，CD⊥AB ，垂足为D ，则：（1）CD²＝AD•BD ，（2）AC²＝AB•AD ，（3）BC²＝AB•BD；请你证明定理中的结论（2）BC²＝AB•BD ．
  
  【结论运用】
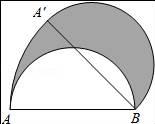
2. （2）如图2，正方形ABCD的边长为6，点O是对角线AC、BD的交点，点E在CD上，过点C作CF⊥BE ，垂足为F ，连接OF ，
  ①求证：△BOF∽△BED；
  
  ②若BE＝2 $\text{[math]}$ ，求OF的长．
答案解析收藏纠错 + 选题
25. (2019·云霄模拟) 如图，二次函数y＝ax²+bx+c（a≠0）的图象交x轴于A、B两点，交y轴于点D ，点B的坐标为（3，0），顶点C的坐标为（1，4）．
1. （1）求二次函数的解析式和直线BD的解析式；
2. （2）点P是直线BD上的一个动点，过点P作x轴的垂线，交抛物线于点M ，当点P在第一象限时，求线段PM长度的最大值；
3. （3）在抛物线上是否存在异于B、D的点Q ，使△BDQ中BD边上的高为2 $\text{[math]}$ ？若存在求出点Q的坐标；若不存在请说明理由．
答案解析收藏纠错 + 选题