![]()


 B .
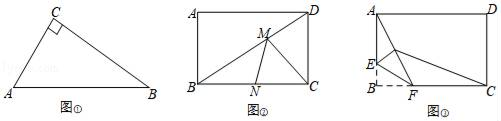
B . 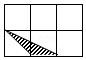 C .
C . 
①图象一定经过(2,﹣1);②图象经过一、二、四象限;③与坐标轴围成的三角形面积为12.5;④x每增加1,y的值减少2;⑤该图象向左平移1个单位后的函数表达式是y=﹣2x+4,正确是( )
 B .
B .  C .
C .  D .
D . 
①阴影部分的周长为4;②当k= 时,图中阴影部分为正六边形;③当k=
时,图中阴影部分的面积是
.


解关于x的不等式: ﹣
≤f(3)+f(4)+…+f(11),并将解集在数轴上表示出来.
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
|
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
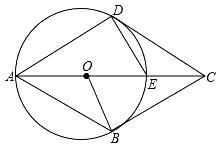
①若点P的纵坐标为2,求直线AB的函数表达式.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.