





请解答下列问题:
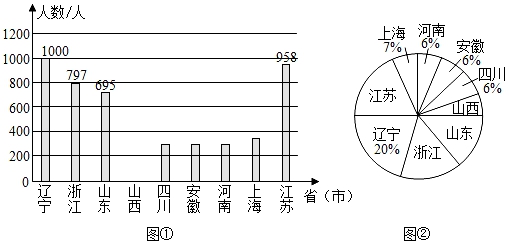
②请将条形统计图补充完整;

问题提出:
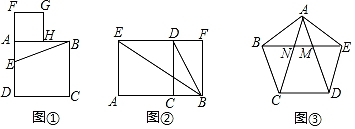
如图①是三世佛的中央坐像,请你设计方案并求出它的高度.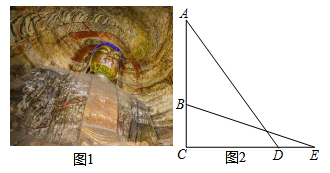
方案设计:
如图②,该课题研究小组通过研究设计了这样一个方案,某同学在D处用测角器测得佛像最高处A的仰角∠ADC=40°,另一个同学在他的后方2.14m的E处测得佛像底端B的仰角∠BEC=10°.
数据收集:
通过查阅资料和实际测量:佛像底端到观景台的垂直距离BC为5m .
问题解决:
黄金分割
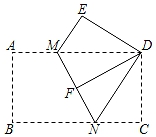
天文学家开普勒把黄金分割称为神圣分割,并指出毕达哥拉斯定理(勾股定理)和黄金分割是几何中的双宝,前者好比黄金,后者堪称珠宝,历史上最早正式在书中使用“黄金分割”这个名称的是欧姆,19世纪以后“黄金分割”的说法逐渐流行起来,黄金分割被广泛应用于建筑等领域.黄金分割指把一条线段分为两部分,使其中较长部分与线段总长之比等于较短部分与较长部分之比,该比值为 ,用下面的方法(如图①)就可以作出已知线段AB的黄金分割点H:
①以线段AB为边作正方形ABCD ,
②取AD的中点E , 连接EB ,
③延长DA到F , 使EF=EB ,
④以线段AF为边作正方形AFGH , 点H就是线段AB的黄金分割点.
以下是证明点H就是线段AB的黄金分割点的部分过程:
证明:设正方形ABCD的边长为1,则AB=AD=1,
∵E为AD中点,
∴AE= ,
∴在Rt△BAE中,BE=
∵EF=BE
∴EF=
∴AF=EF﹣AE= ,
…
任务:
问题情境
数学活动课上,老师让同学们以“三角形的旋转”为主题开展数学活动,△ABC和△DEC是两个全等的直角三角形纸片,其中∠ACB=∠DCE=90°,∠B=∠E=30°,AB=DE=4.
解决问题

探索发现