15.
(2020九下·宝应模拟)
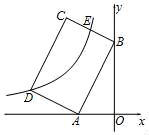
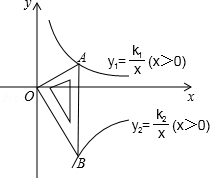
如图,帆船A和帆船B在太湖湖面上训练,O为湖面上的一个定点,教练船静候于O点,训练时要求A、B两船始终关于O点对称.以O为原点,建立如图所示的坐标系,x轴、y轴的正方向分别表示正东、正北方向.设A、B两船可近似看成在双曲线y=

上运动,湖面风平浪静,双帆远影优美,训练中当教练船与A、B两船恰好在直线y=x上时,三船同时发现湖面上有一遇险的C船,此时教练船测得C船在东南45°方向上,A船测得AC与AB的夹角为60°,B船也同时测得C船的位置(假设C船位置不再改变,A、B、C三船可分别用A、B、C三点表示).
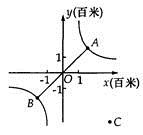
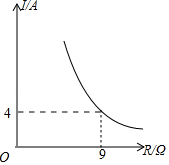
 B .
B .  C .
C .  D .
D . 
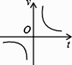 B .
B .  C .
C .  D .
D .