浙江省宁波七中教育集团2019-2020学年九年级下学期数学...

更新时间：2024-07-13 浏览次数：331 类型：月考试卷

一、选择题(每小题4分，共48分)

1. (2020九下·宁波月考) -3的倒数等于（）

A . 9 B . -3 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020九下·宁波月考) 下列计算正确的是（）

A . x+x=2x² B . x-x=1 C . x·x=x² D . x÷x= 0

答案解析收藏纠错 + 选题
3. (2020九下·宁波月考) 截止2020年4月12日，本次新冠病毒感染病例美国超55万人，其中55万用科学记数法表示为（）

A . 5.5x10⁵ B . 55×10⁴ C . 5.5×10⁴ D . 0.55×10⁶

答案解析收藏纠错 + 选题
4. (2020九下·宁波月考) 由5个大小相同的正方体组成的几何体如图所示，其主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2020九下·宁波月考) 一组数据1，1，1，3，5，7，现加入一个整数a，一定不会发生变化的统计量是（）

A . 平均数 B . 中位数 C . 众数 D . 方差

答案解析收藏纠错 + 选题
6. (2020九下·宁波月考) 满足不等式组 $\text{[math]}$ 整数解的和是（）

A . 2 B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题
7. (2020九下·宁波月考) 如图，∠AOB=100°，点C在⊙O上，且点C不与A，B重合，则∠ACB的度数为（）

A . 50° B . 80°或50° C . 130° D . 50°或130°

答案解析收藏纠错 + 选题
8. (2020九下·宁波月考) 如图，飞镖游戏板中每一块小正方形除颜色外都相同。若一个人向游戏板投掷飞镖一次(假设飞镖落在游戏板上)，则飞镖落在阴影部分的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2020九下·宁波月考) “赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形。如果小正方形的面积为4，大正方形的面积为100，直角三角形中较小的锐角为α，则tanα的值等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024九上·扶余期末) 《九章算术》是我国古代著名数学著作，书中记载：“今有圆材，埋在壁中，不知大小以锯锯之，深一寸，锯道长一尺，问径几何？”用数学语言可表述为：“如图，CD为⊙O的直径，弦AB⊥DC于E，ED=1寸，AB=10寸，求直径CD的长。”则CD为（）

A . 10寸 B . 3寸 C . 20寸 D . 26寸

答案解析收藏纠错 + 选题
11. (2020九下·宁波月考) 如图，∠A=∠B=∠C=∠D=∠E=∠F=60°，AB=3，BC=DE=1，CD=2，EF=0.5，则AG的长是（）

A . 5.5 B . 6 C . 6.5 D . 7

答案解析收藏纠错 + 选题
12. (2020九下·宁波月考) 一个大矩形按如图方式分割成16个小矩形，且只有标号为①②③的三个大小不同的小矩形为正方形，在满足条件的所有分割中，若知道16个小矩形中n个小矩形的周长，就一定能算出这个大矩形的面积，则n的最小值是（）

A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题

二、填空题(每小题4分，共24分)

13. (2020九下·宁波月考) 在-2，2， $\text{[math]}$ 这三个实数中，最小的是。

答案解析收藏纠错 + 选题
14. (2023·拱墅模拟) 因式分解：x²-x=．

答案解析收藏纠错 + 选题
15. (2020九下·宁波月考) 将抛物线y=x²先向上平移2个单位，再向左平移4个单位后的抛物线的解析式是。

答案解析收藏纠错 + 选题
16. (2020九下·宁波月考) 有一个只含有x的代数式，x的值与代数式的值对应如下表：

x

0

1

2

代数式的值

2

1

2

请写出两个符合上述条件的代数式，它可以是和。

答案解析收藏纠错 + 选题
17. (2020九下·宁波月考) 如图，在△ABC中，AB=AC， BC=12，E为AC的中点，线段BE的垂直平分线交边BC于D，设tan∠ACB=x，BD=y，则y与x的函数关系式是。

答案解析收藏纠错 + 选题
18. (2020九下·宁波月考) 如图，在Rt△AOB中，∠AOB=90°，AO=3，BO=4，将△AOB绕顶点O逆时针旋转α(0<α<90°)，得到△A'OB'，A'B'与OB相交于点E，若△OA'E为等腰三角形，则线段B'E的长度为。

答案解析收藏纠错 + 选题

三、解答题(本大题有8小题，共78分)

19. (2020九下·宁波月考) 计算： $\text{[math]}$ -(π-2020)⁰+|2 $\text{[math]}$ -2|- $\text{[math]}$ 。

答案解析收藏纠错 + 选题
20. (2020九下·宁波月考) 如图正方形网格中，每个小正方形的边长都为1。请在所给网格中按下列要求画出图形。
1. （1）在图1中以AB为边画一个等腰三角形ABC，使C在格点上，且另两边的长都是无理数；
2. （2）在图2中以AB为边画一个凸多边形，使多边形各顶点都在格点上且是中心对称图形，并且各边长都是无理数。
答案解析收藏纠错 + 选题
21. (2020九下·宁波月考) 某学校环保小组为了解游客在某园区内购买瓶装饮料数量的情况，一天他们分别在A、B、C三个出口处，对离开园区的游客进行调查，其中在A出口调查所得的数据整理后绘成图1。

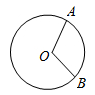
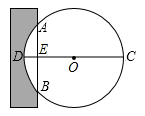
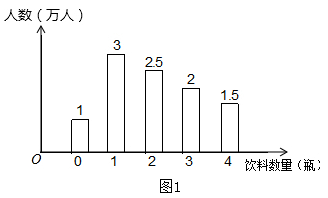
图2表一

出口

B

C

人均购买饮料数量(瓶)

3

2
1. （1）在A出口的被调查游客中，购买2瓶及2瓶以上饮料的游客人数占A出口的被调查游客人数的%。
2. （2）求A出口的被调查游客在园区内人均购买了多少瓶饮料？
3. （3）已知B、C两个出口的被调查游客在园区内人均购买饮料的数量如表一(图2)所示，若C出口的被调查人数比B出口的被调查人数多2万，B、C两个出口的被调查游客在园区内共购买了49万瓶饮料，试问B出口的被调查游客人数为多少万？
答案解析收藏纠错 + 选题
22. (2020九下·宁波月考) 图1是一种折叠门，由上下轨道和两扇长宽相等的活页门组成，整个活页门的右轴固定在门框上，通过推动左侧活页门开关。图2是其俯视简化示意图，已知轨道AB=120cm，两扇活页门的宽OC=OB=60cm，点B固定，当点C在AB上左右运动时，OC与OB的长度不变。
1. （1）若∠OBC=53°，求AC的长。
  (结果保留整数，参考数据：sin53°≈0.8，cos53°≈0.6，tan53°≈1.3)
2. （2）当点C从点A向右运动60cm时，求点O在此过程中运动的路径长。
答案解析收藏纠错 + 选题
23. (2020九下·宁波月考) 已知一次函数y=kx+2的图象与反比例函数y= $\text{[math]}$ 的图象交于点P，点P在第一象限。PA⊥x轴于点A，PB⊥y轴于点B。一次函数的图象分别交x轴、y轴于点C、D，且S_△PBD=4， $\text{[math]}$ 。
1. （1）求点D的坐标；
2. （2）求一次函数与反比例函数的解析式；
3. （3）直接写出当x>0时，一次函数的值大于反比例函数的值的x的取值范围。
答案解析收藏纠错 + 选题
24. (2020九下·宁波月考) 空地上有一段长为20m的旧墙MN，小敏利用旧墙和木栏围成一个矩形菜园ABCD，已知木栏总长100m。设AD=x(m)，矩形菜园ABCD的面积为y(m²) ．
1. （1）若x≤20，如图1，矩形菜园的一边靠墙，另三边一共用了100m木栏。
  ①求y关于x的函数表达式，并写出自变量x的取值范围。
  
  ②当AD为多少米时，矩形菜园ABCD的面积最大，并求出最大值。
2. （2）若x>20，如图2，且空地足够大，请你合理利用旧墙及所给木栏，帮小敏设计一个方案，使得所围成的矩形菜园ABCD的面积最大，并求出最大值。
答案解析收藏纠错 + 选题
25. (2020九下·宁波月考) 如果一个三角形的两个内角α，β满足α+2β=90°，那么我们称这样的三角形为“非常三角形”。
1. （1）若△ABC是“非常三角形”，∠C>90°，∠A=50°，则∠B=。
2. （2）如图，△ABC中，AB=AC，D是边BC上一点，以BD为直径的⊙O经过点A，连结AD。
  ①求证：△ADC为“非常三角形”。
  
  ②若sin B= $\text{[math]}$ ，AB=8，弦AB上是否存在一点P，使得△BDP是“非常三角形”，若存在，请求出线段AP的长度；若不存在，请说明理由。
答案解析收藏纠错 + 选题
26. (2020九下·宁波月考) 如图，在平面直角坐标系xOy中，抛物线y=ax²+bx+c与x轴交于点A(2，0)、B(6，0)，与y轴交于点C(0，6)，顶点为D，连结AC，作直线BC，点E是抛物线对称轴上的一个动点。
1. （1）求出抛物线的解析式。
2. （2）若∠BCE=∠OCA，求点E的坐标。
3. （3）在(2)的条件下，延长CE交抛物线于点F，直接写出所有满足△GBD∽△FBC的点G的坐标。
答案解析收藏纠错 + 选题