吉林省长春市农安县2018-2019学年八年级下学期期末考试...

更新时间：2024-07-13 浏览次数：221 类型：期末考试

一、选择题

1. (2019八下·农安期末) 无论 $\text{[math]}$ 取什么数，总有意义的分式是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2019八下·农安期末) 若(x﹣2)^x＝1，则x的值是（）

A . 0 B . 1 C . 3 D . 0或3

答案解析收藏纠错 + 选题
3. (2019八下·农安期末) 如图所示，一次函数 $\text{[math]}$ 的图像可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2024八下·集宁期末) 为了调查某种小麦的长势，从中抽取了10株麦苗，测得苗高（单位： $\text{[math]}$ ）为16，9，14，11，12，10，16，8，17，19，则这组数据的中位数和众数分别是（）

A . 11，11 B . 12，11 C . 13，11 D . 13，16

答案解析收藏纠错 + 选题
5. (2019八下·农安期末) 无论a取何值，关于x的函数y＝﹣x+a²+1的图象都不经过（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
6. (2019八下·农安期末) 如图，直线 $\text{[math]}$ 交坐标轴于 $\text{[math]}$ 、 $\text{[math]}$ 两点，则不等式 $\text{[math]}$ 的解集为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2019八下·农安期末) 如图，平行四边形ABCD的对角线AC、BD相交于点O，下列结论正确的是（　　）

A . S_▱_ABCD=4S_△_AOB B . AC=BD C . AC⊥BD D . ▱ABCD是轴对称图形

答案解析收藏纠错 + 选题
8. (2023八下·安达期末) 如图，将▱ABCD沿对角线AC折叠，使点B落在B′处，若∠1=∠2=44°，则∠B为（）

A . 66° B . 104° C . 114° D . 124°

答案解析收藏纠错 + 选题

二、填空题

9. (2019八下·农安期末) 用科学记数法表示： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
10. (2019八下·农安期末) 根据如图所示的程序，当输入x＝3时，输出的结果y＝.

答案解析收藏纠错 + 选题
11. (2024八下·成都期末) 若关于 $\text{[math]}$ 的方程 $\text{[math]}$ 无解，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
12. (2019八下·农安期末) 现有甲、乙两支篮球队，每支球队队员身高的平均数均为1.85米，方差分别为 $\text{[math]}$ ， $\text{[math]}$ ，则身高较整齐的球队是队．

答案解析收藏纠错 + 选题
13. (2019八下·农安期末) 如图，▱ABCD与▱DCFE的周长相等，且∠BAD=60°，∠F=110°，则∠DAE的度数为°．

答案解析收藏纠错 + 选题
14. (2019八下·农安期末) 点A在双曲线y= $\text{[math]}$ 上，点B在双曲线y= $\text{[math]}$ （k≠0）上，AB∥x轴，分别过点A、B向x轴作垂线，垂足分别为D、C，若矩形ABCD的面积是8，则k的值为．

答案解析收藏纠错 + 选题

三、综合题

15. (2019八下·农安期末) 解方程： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2019八下·农安期末) 以下是小明化简分式 $\text{[math]}$ 的过程．
解：原式

$\text{[math]}$                               ①

$\text{[math]}$                                     ②

$\text{[math]}$                                           ③

$\text{[math]}$                                                      ④
1. （1）小明的解答过程在第步开始出错；
2. （2）请你帮助小明写出正确的解答过程，并计算当 $\text{[math]}$ 时分式的值．
答案解析收藏纠错 + 选题
17. (2019八下·农安期末) 甲、乙两个工程队合作完成一项工程，两队合做2天后由乙队单独做1天就完成了全部工程，已知乙队单独做所需的天数是甲队单独做所需天数的1.5倍，求甲、乙两队单独做各需多少天完成该项工程？

答案解析收藏纠错 + 选题
18. (2019八下·农安期末) 如图， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，求证：四边形 $\text{[math]}$ 是菱形．

答案解析收藏纠错 + 选题
19. (2019八下·农安期末) 如图，点 A，B，C，D 依次在同一条直线上，点 E，F 分别在直线 AD 的两侧，已知 BE//CF，∠A=∠D，AE=DF.
1. （1）求证：四边形 BFCE 是平行四边形.
2. （2）若 AD=10，EC=3，∠EBD=60°，当四边形 BFCE是菱形时，求 AB 的长.
答案解析收藏纠错 + 选题
20. (2019八下·农安期末) 如图，在平面直角坐标系中，四边形ABCD是矩形，AD∥x轴，A（ $\text{[math]}$ ， $\text{[math]}$ ），AB=1，AD=2．
1. （1）直接写出B、C、D三点的坐标；
2. （2）将矩形ABCD向右平移m个单位，使点A、C恰好同时落在反比例函数 $\text{[math]}$ （ $\text{[math]}$ ）的图象上，得矩形A′B′C′D′．求矩形ABCD的平移距离m和反比例函数的解析式．
答案解析收藏纠错 + 选题

21. (2022八下·侯马期末) 我市某中学举行“中国梦•校园好声音”歌手大赛，高、初中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

（1）根据图示填写下表；

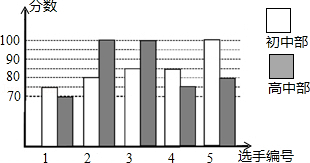
	平均数（分）	中位数（分）	众数（分）
初中部		85
高中部	85		100

（2）结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；
（3）计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.

答案解析收藏纠错 + 选题

22. (2023·株洲模拟) 如图，点E是正方形ABCD外一点，点F是线段AE上一点，△EBF是等腰直角三角形，其中∠EBF=90°，连接CE、CF．
1. （1）求证：△ABF≌△CBE；
2. （2）判断△CEF的形状，并说明理由．
答案解析收藏纠错 + 选题
23. (2019八下·农安期末) 某中学举行春季长跑比赛活动，小明从起点学校西门出发，途经市博物馆后按原路返还，沿比赛路线跑回终点学校西门．设小明离开起点的路程s（千米）与跑步时间t（分钟）之间的函数关系如图所示，其中从起点到市博物馆的平均速度是0.3千米/分钟，用时35分钟根据图象提供的信息，解答下列问题：
1. （1）求图中 $\text{[math]}$ 的值，并求出 $\text{[math]}$ 所在直线方程；
2. （2）组委会在距离起点2.1千米处设立一个拍摄点 $\text{[math]}$ ，小明从第一次过点 $\text{[math]}$ 到第二次经过点 $\text{[math]}$ 所用的时间为68分钟
  ①求 $\text{[math]}$ 所在直线的函数解析式；
  
  ②该运动员跑完赛程用时多少分钟？
答案解析收藏纠错 + 选题
24. (2020九上·济宁期中) 定义：对于给定的两个函数,任取自变量x的一个值,当x<0时,它们对应的函数值互为相反数;当x⩾0时,它们对应的函数值相等,我们称这样的两个函数互为相关函数。例如：一次函数y=x−1,它们的相关函数为y= $\text{[math]}$ .
1. （1）已知点A(−5,8)在一次函数y=ax−3的相关函数的图象上，求a的值；
2. （2）已知二次函数y=−x $\text{[math]}$ +4x− $\text{[math]}$ .
  ①当点B(m, $\text{[math]}$ )在这个函数的相关函数的图象上时，求m的值；
  
  ②当−3⩽x⩽3时,求函数y=−x $\text{[math]}$ +4x− $\text{[math]}$ 的相关函数的最大值和最小值.
答案解析收藏纠错 + 选题