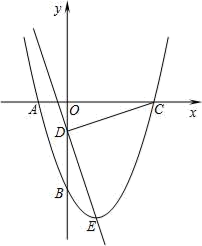
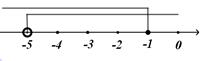
 B .
B .  C .
C . 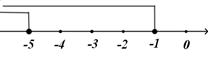 D .
D . 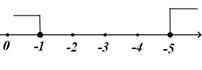
 B .
B .  C .
C . 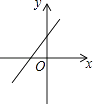 D .
D . 
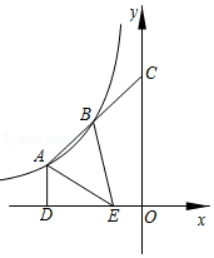

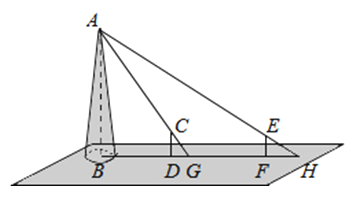
如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,则建筑物的高是 米.
|
列 行 |
第1列 |
第2列 |
第3列 |
第4列 |
|
第1行 |
1 |
2 |
3 |
4 |
|
第2行 |
8 |
7 |
6 |
5 |
|
第3行 |
9 |
10 |
11 |
12 |
|
第4行 |
16 |
15 |
14 |
13 |
|
… |
… |
… |
… |
… |
|
第 | … | … | … | … |
规定位于第 行,第
列的自然数10记为
,自然数15记为
…按此规律,自然数2018记为.
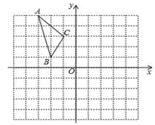
①若 经过平移后得到
,已知点
的坐标为
,写出顶点
的坐标,画出
;
②若 和
关于原点
成中心对称图形,写出
的各顶点的坐标;
③将 绕着点
按顺时针方向旋转
得到
,写出
的各顶点的坐标,并画出
.
①公司将笔试成绩(百分制)分成了四组,分别为A组:60≤x<70,B组:70≤x<80,C组:80≤x<90,D组:90≤x<100;并绘制了如下的笔试成绩频数分布直方图.其中,C组的分数由低到高依次为:80,81,82,83,83,84,84,85,86,88,88,88,89.
②这些大学生的笔试、面试成绩的平均数、中位数、众数、最高分如下表:
|
平均数 |
中位数 |
众数 |
最高分 |
|
|
笔试成绩 |
81 |
m |
92 |
97 |
|
面试成绩 |
80.5 |
84 |
86 |
92 |
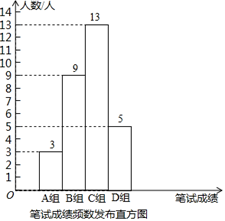
根据以上信息,回答下列问题: