
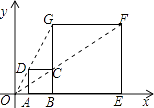
 B .
B .  D .
D . 


| 组别 | 课前预习时间 | 频数(人数) | 频率 |
| 1 | | 2 | |
| 2 | | | 0.10 |
| 3 | | 16 | 0.32 |
| 4 | | | |
| 5 | | 3 |
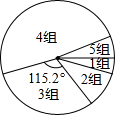
请根据图表中的信息,回答下列问题:
| 第一次 | 第二次 | |
| | 20 | 30 |
| | 30 | 40 |
| 累计采购款/元 | 10200 | 14400 |
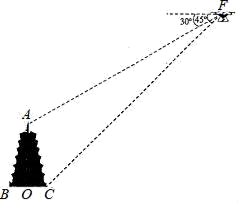

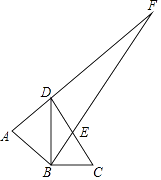
问题解决