北京理工附中2020年中考数学三模试卷

更新时间：2021-05-20 浏览次数：215 类型：中考模拟

一、单选题

1. (2020·北京模拟) 2019年10月1日，约120 000名群众观看了天安门广场的升旗仪式．将120 000用科学记数法表示应为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020·北京模拟) 下列四个图形依次是北京、云南、西藏、安徽四个省市的图案字体，其中是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2020八上·松山期中) 六边形的外角和是（）

A . 360° B . 540° C . 720° D . 900°

答案解析收藏纠错 + 选题
4. (2020·北京模拟) 下列几何体中，主视图和左视图完全相同的图形的有几个（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
5. (2020九上·武汉月考) 用配方法解方程 $\text{[math]}$ ，配方后的方程是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020·北京模拟) 如图，直线 $\text{[math]}$ 直线 $\text{[math]}$ 分别与 $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，且与 $\text{[math]}$ 的平分线交于 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . 35° B . 30° C . 55° D . 20°

答案解析收藏纠错 + 选题
7. (2020·杭州模拟) 二十四节气是中国古代劳动人民长期经验积累的结品，它与白昼时长密切相关．当春分、秋分时，昼夜时长大致相等；当夏至时，白昼时长最长．下图是一年中部分节气所对应的白昼时长示意图．在下列选项中白昼时长超过14小时的节气是（）

A . 惊蛰 B . 立夏 C . 夏至 D . 大寒

答案解析收藏纠错 + 选题
8. (2020·北京模拟) 图1是2020年3月26日全国新冠疫情数据表，图2是3月28日海外各国疫情统计表，图3是中国和海外的病死率趋势对比图，根据这些图表，选出下列说法中错误的一项（）

A . 图1显示每天现有确诊数的增加量=累计确诊增加量-治愈人数增加量-死亡人数增加量． B . 图2显示美国累计确诊人数虽然约是德国的两倍，但每百万人口的确诊人数大约只有德国的一半． C . 图2显示意大利当前的治愈率高于西班牙． D . 图3显示大约从3月16日开始海外的病死率开始高于中国的病死率

答案解析收藏纠错 + 选题

二、填空题

9. (2020·湖州模拟) 分解因式： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
10. (2020·北京模拟) 在平面直角坐标系 $\text{[math]}$ 中，将点 $\text{[math]}$ 绕原点 $\text{[math]}$ 顺时针旋转90°，所得到的对应点的坐标为．

答案解析收藏纠错 + 选题
11. (2020·北京模拟) 已知函数满足下列两个条件：①当 $\text{[math]}$ 时， $\text{[math]}$ 随 $\text{[math]}$ 的增大而减小；②它的图象经过坐标原点，请写出一个符合上述条件的函数的表达式．

答案解析收藏纠错 + 选题
12. (2020·北京模拟) 如图， $\text{[math]}$ ， $\text{[math]}$ 相交于 $\text{[math]}$ 点， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题
13. (2020·北京模拟) 如图，在平面直角坐标系 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，双曲线 $\text{[math]}$ 与线段 $\text{[math]}$ 无公共点，则 $\text{[math]}$ 的取值范围是．

答案解析收藏纠错 + 选题
14. (2020·北京模拟) 在数学课上，老师提出如下问题：
尺规作图：过直线外一点作已知直线的平行线．
已知：直线l及其外一点A．
求作：l的平行线，使它经过点A．
小云的作法如下：
⑴在直线l上任取一点B；
⑵以B为圆心，BA长为半径作弧，交直线l于点C；
⑶分别以A，C为圆心，BA长为半径作弧，两弧相交于点D；
⑷作直线AD．直线AD即为所求．
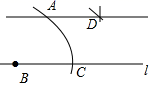
小云作图的依据是．

答案解析收藏纠错 + 选题

15. (2020·北京模拟) 某超市随机选取1000位顾客，记录了他们购买甲、乙、丙、丁四种商品的情况，整理成如下统计表，其中“√”表示购买，“×”表示未购买．假定每位顾客购买商品的可能性相同．

商品顾客人数	甲	乙	丙	丁
100	√	×	√	√
217	×	√	×	√
200	√	√	√	×
300	√	×	√	×
85	√	×	×	×
98	×	√	×	×

（1）估计顾客同时购买乙和丙的概率为．
（2）如果顾客购买了甲，并且同时也在乙、丙、丁中进行了选购，则购买（填乙、丙、丁）商品的可能性最大．

答案解析收藏纠错 + 选题

16. (2020·北京模拟) 上图为2009年到2015年中关村国家自主创新示范区企业经营技术收入的统计图．
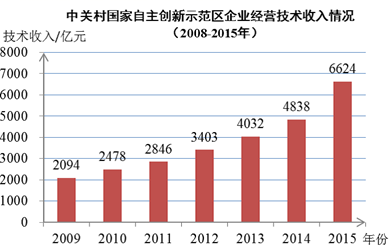
下面四个推断：

①2009年到2015年技术收入持续增长；

②2009年到2015年技术收入的中位数是3403亿；

③2009年到2015年技术收入增幅最大的是2015年；

④2009年到2011年的技术收入平均增长率比2013年到2015年技术收入平均增长率大．

其中，正确的是．

答案解析收藏纠错 + 选题

三、解答题

17. (2020·北京模拟) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
18. (2020·北京模拟) 先化简： $\text{[math]}$ ，再从 $\text{[math]}$ 的整数中选取一个你喜欢的 $\text{[math]}$ 的值代入求值．

答案解析收藏纠错 + 选题
19. (2020·北京模拟) 如图所示， $\text{[math]}$ 是 $\text{[math]}$ 的平分线， $\text{[math]}$ ，垂足为 $\text{[math]}$ ， $\text{[math]}$ ，垂足为 $\text{[math]}$ ，且 $\text{[math]}$ ．
求证： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
20. (2023九上·西安期末) 已知关于 $\text{[math]}$ 的方程 $\text{[math]}$ ．
1. （1）若该方程有两个不相等的实数根，求实数 $\text{[math]}$ 的取值范围：
2. （2）当该方程的一个根为-3时，求 $\text{[math]}$ 的值及方程的另一根．
答案解析收藏纠错 + 选题
21. (2020·北京模拟) 如图，在矩形 $\text{[math]}$ 中，对角线 $\text{[math]}$ 的垂直平分线 $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ，与 $\text{[math]}$ 相交于点 $\text{[math]}$ ．连接 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证：四边形 $\text{[math]}$ 是菱形；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
22. (2020·北京模拟) 小辉为了解市政府调整水价方案的社会反响，随机访问了自己居住在小区的部分居民，就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查，并把调查结果整理成下面的图1，图2．

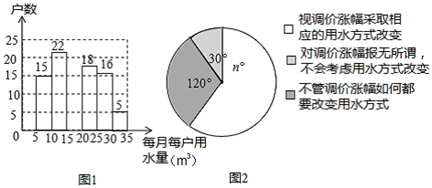
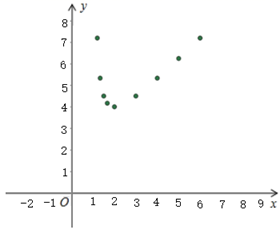
小辉发现每月每户的用水量在 $\text{[math]}$ 之间，有7户居民对用水价格调价涨幅抱无所谓，不用考虑用水方式的改变．根据小军绘制的图表和发现的信息，完成下列问题：
1. （1） $\text{[math]}$ ，小明调查了户居民，并补全图1；
2. （2）每月每户用水量的中位数落在之间，众数落在之间；
3. （3）如果小明所在的小区有1200户居民，请你估计“视调价涨幅采取相应的用水方式改变”的居民户数多少?
答案解析收藏纠错 + 选题
23. (2020·北京模拟) 如图，已知 $\text{[math]}$ ，以 $\text{[math]}$ 为直径的 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，点 $\text{[math]}$ 为弧 $\text{[math]}$ 的中点，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ．且 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；
2. （2）若 $\text{[math]}$ 的半径为4， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
24. (2020·北京模拟) 在平面直角坐标系 $\text{[math]}$ 中，函数 $\text{[math]}$ （ $\text{[math]}$ ）的图象 $\text{[math]}$ 经过点 $\text{[math]}$ （4，1），直线 $\text{[math]}$ 与图象 $\text{[math]}$ 交于点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 的值；
2. （2）横、纵坐标都是整数的点叫做整点．记图象 $\text{[math]}$ 在点 $\text{[math]}$ ， $\text{[math]}$ 之间的部分与线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 围成的区域（不含边界）为 $\text{[math]}$ ．
  ①当 $\text{[math]}$ 时，直接写出区域 $\text{[math]}$ 内的整点个数；
  ②若区域 $\text{[math]}$ 内恰有4个整点，结合函数图象，求 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
25. (2020·北京模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ，为了研究图中线段之间的关系，设 $\text{[math]}$ ， $\text{[math]}$ ，
1. （1）可通过证明 $\text{[math]}$ ，得到 $\text{[math]}$ 关于 $\text{[math]}$ 的函数表达式 $\text{[math]}$ ，其中自变量 $\text{[math]}$ 的取值范围是；
2. （2）根据图中给出的（1）中函数图象上的点，画出该函数的图象；
3. （3）借助函数图象，回答下列问题：① $\text{[math]}$ 的最小值是；②已知当 $\text{[math]}$ 时， $\text{[math]}$ 的形状与大小唯一确定，借助函数图象给出 $\text{[math]}$ 的一个估计值（精确到0.1）或者借助计算给出 $\text{[math]}$ 的精确值．
答案解析收藏纠错 + 选题
26. (2020·北京模拟) 在平面直角坐标系 $\text{[math]}$ 中，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ，将点 $\text{[math]}$ 向右平移某个距离得到点 $\text{[math]}$ ，点 $\text{[math]}$ 在抛物线上．已知点 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）当 $\text{[math]}$ 时．
  ①求点 $\text{[math]}$ 的坐标（用含 $\text{[math]}$ 的式子表示）；
  
  ②求线段 $\text{[math]}$ 的长度；
2. （2）若抛物线与线段 $\text{[math]}$ 恰有一个公共点，结合函数图象，求 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
27. (2020·北京模拟) 如图， $\text{[math]}$ 中， $\text{[math]}$ ． $\text{[math]}$ ．将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转60°到点 $\text{[math]}$ ，点 $\text{[math]}$ 与点 $\text{[math]}$ 关于直线 $\text{[math]}$ 对称，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）依题意补全图形：
2. （2）判断 $\text{[math]}$ 的形状，并证明你的结论；
3. （3）请问在直线 $\text{[math]}$ 上是否存在点 $\text{[math]}$ ．使得 $\text{[math]}$ 恒成立若存在，请用文字描述出点 $\text{[math]}$ 的准确位置，并画图证明；若不存在，请说明理由．
答案解析收藏纠错 + 选题
28. (2020·北京模拟) 对于平面内的点 $\text{[math]}$ 和点 $\text{[math]}$ ，给出如下定义：点 $\text{[math]}$ 为平面内一点，若点 $\text{[math]}$ 使得 $\text{[math]}$ 是以 $\text{[math]}$ 为顶角且 $\text{[math]}$ 小于90°的等腰三角形，则称点 $\text{[math]}$ 是点 $\text{[math]}$ 关于点 $\text{[math]}$ 的锐角等腰点．如图，点 $\text{[math]}$ 是点 $\text{[math]}$ 关于点 $\text{[math]}$ 的锐角等腰点．

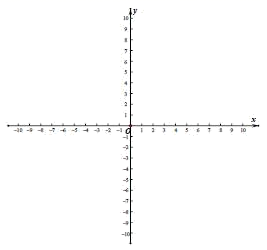
在平面直角坐标系xOy中，点O为坐标原点
1. （1）已知点 $\text{[math]}$ ，在点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 中，是点 $\text{[math]}$ 关于点 $\text{[math]}$ 的锐角等腰点的是；
2. （2）已知点 $\text{[math]}$ ，点 $\text{[math]}$ 在直线 $\text{[math]}$ 上，若点 $\text{[math]}$ 是点 $\text{[math]}$ 关于点 $\text{[math]}$ 的锐角等腰点，求实数 $\text{[math]}$ 的取值范围．
3. （3）点 $\text{[math]}$ 是 $\text{[math]}$ 轴上的动点， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 是以点 $\text{[math]}$ 为圆心，2为半径的圆上一动点．且满足 $\text{[math]}$ ，若直线 $\text{[math]}$ 上存在点 $\text{[math]}$ 关于点 $\text{[math]}$ 的锐角等腰点，请直接写出 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题