湖北省随州市随县2018-2019学年七年级下学期数学期末考...

更新时间：2020-07-30 浏览次数：186 类型：期末考试

一、选择题

1. (2019·宝鸡模拟) ﹣ $\text{[math]}$ 的立方根是（　　）

A . ﹣ $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . ﹣ $\text{[math]}$

答案解析收藏纠错 + 选题
2. 如果a＜b，那么下列各式一定正确的是（）

A . a²＜b² B . $\text{[math]}$ C . ﹣2a＞﹣2b D . a﹣1＞b﹣1

答案解析收藏纠错 + 选题
3. (2017七下·高阳期末) 下列调查中，调查方式选择合理的是（）

A . 为了了解某一品牌家具的甲醛含量，选择全面调查； B . 为了了解神舟飞船的设备零件的质量情况，选择抽样调查； C . 为了了解某公园全年的游客流量，选择抽样调查； D . 为了了解一批袋装食品是否含有防腐剂，选择全面调查.

答案解析收藏纠错 + 选题
4. 下列结论正确的是（）

A . 64的立方根是 $\text{[math]}$ B . $\text{[math]}$ 没有立方根 C . 立方根等于本身的的数是0 D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2019七下·华蓥期末) 如图，已知AB∥CD，∠2＝100°，则下列正确的是（）

A . ∠1＝100° B . ∠3＝80° C . ∠4＝80° D . ∠4＝100°

答案解析收藏纠错 + 选题
6. 若点M（a﹣2，2a+3）是y轴上的点，则a的值是（）

A . 2 B . ﹣ $\text{[math]}$ C . ﹣2 D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2017七下·曲阜期中) 如图，直线a、b被直线c所截，下列说法正确的是（）

A . 当∠1=∠2时，一定有a∥b B . 当a∥b时，一定有∠1=∠2 C . 当a∥b时，一定有∠1+∠2=90° D . 当∠1+∠2=180°时，一定有a∥b

答案解析收藏纠错 + 选题
8. (2019七下·孝南期末) 把不等式组 $\text{[math]}$ 的解集表示在数轴上，下列选项正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
9. 如图，直线 $\text{[math]}$ ，将 $\text{[math]}$ ( $\text{[math]}$ )的直角顶点 $\text{[math]}$ 放在直线 $\text{[math]}$ 上，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2019七下·华蓥期末) 如果关于 $\text{[math]}$ 的方程组 $\text{[math]}$ 的解是正数，那a的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 无解

答案解析收藏纠错 + 选题

二、填空题

11. (2017七下·荔湾期末) 若P（4，﹣3），则点P到x轴的距离是．

答案解析收藏纠错 + 选题
12. 若代数式 $\text{[math]}$ 的值不小于代数式 $\text{[math]}$ 的值，则x的取值范围是.

答案解析收藏纠错 + 选题
13. 如图，直线a、b被直线c所截，若满足，则a、b平行.

答案解析收藏纠错 + 选题
14. 若买2支圆珠笔、1本日记本需4元；买1支圆珠笔、2本日记本需5元，则买4支圆珠笔、4本日记本需元.

答案解析收藏纠错 + 选题
15. (2019七下·恩施期末) 如图，小章利用一张左、右两边已经破损的长方形纸片 $\text{[math]}$ 做折纸游戏，他将纸片沿 $\text{[math]}$ 折叠后，D、C两点分别落在 $\text{[math]}$ 、 $\text{[math]}$ 的位置，并利用量角器量得 $\text{[math]}$ ，则 $\text{[math]}$ 等于度.

答案解析收藏纠错 + 选题
16. (2019七下·双鸭山期末) 如图，在平面直角坐标系中，一动点从原点O出发，按向上、向右、向下、向右的方向不断地移动，每次移动1个单位长度，得到点A₁（0，1），A₂（1，1），A₃（1，0），A₄（2，0），…，那么点A_{2 019}的坐标为．

答案解析收藏纠错 + 选题

三、解答题

17.
1. （1）解方程组 $\text{[math]}$
2. （2）解不等式，并把它的解集在数轴上表示出来： $\text{[math]}$
答案解析收藏纠错 + 选题
18. 请在横线上填上合适的内容，完成下面的证明：
如图，射线AH交折线ACGFEN于点B、D、E.已知∠A=∠1，∠C=∠F，BM平分∠CBD，EN平分∠FEH.求证：∠2=∠3.

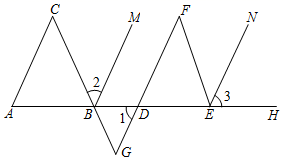
证明：∵∠A=∠1（已知）

∴AC∥GF（ ▲ ）

∴（ ▲ ）（▲ ）

∵∠C=∠F（已知）

∴∠F=∠G

∴（ ▲ ）∥（ ▲ ）

∴（ ▲ ）=（ ▲ ）

∵BM平分∠CBD，EN平分∠FEH

∴∠2=▲ ， ∠3= ▲

∴∠2=∠3

答案解析收藏纠错 + 选题
19. (2016七上·东营期中) 如图，AB交CD于O，OE⊥AB．
1. （1）若∠EOD=20°，求∠AOC的度数；
2. （2）若∠AOC：∠BOC=1：2，求∠EOD的度数．
答案解析收藏纠错 + 选题
20. 如图， $\text{[math]}$ 在直角坐标系中.
1. （1）请写出 $\text{[math]}$ 各点的坐标；
2. （2）求出 $\text{[math]}$ 的面积；
3. （3）将 $\text{[math]}$ 向右平移2个单位，再向下平移3个单位得到的 $\text{[math]}$ ，画出图形，并写出点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的坐标.
答案解析收藏纠错 + 选题
21. (2017七下·鄂州期末) 为传播奥运知识，小刚就本班学生对奥运知识的了解程度进行了一次调查统计：A：熟悉，B：了解较多，C：一般了解．图1和图2是他采集数据后，绘制的两幅不完整的统计图，请你根据图中提供的信息解答以下问题：
1. （1）求该班共有多少名学生；
2. （2）在条形图中，将表示“一般了解”的部分补充完整；
3. （3）在扇形统计图中，计算出“了解较多”部分所对应的圆心角的度数；
4. （4）如果全年级共1000名同学，请你估算全年级对奥运知识“了解较多”的学生人数．
答案解析收藏纠错 + 选题
22. 某商店需要购进甲、乙两种商品共180件其进价和售价如表：（注：获利=售价进价）
1. （1）若商店计划销售完这批商品后能获利1240元，问甲、乙两种商品应分别购进多少件？
2. （2）若商店计划投入资金少于5040元，且销售完这批商品后获利多于1312元，请问有哪几种购货方案？并直接写出其中获利最大的购货方案.
答案解析收藏纠错 + 选题
23. (2019八下·山亭期末) 求不等式（2x﹣1）（x+3）＞0的解集．
解：根据“同号两数相乘，积为正”可得：① $\text{[math]}$ 或 ② $\text{[math]}$ ．

解①得x＞ $\text{[math]}$ ；解②得x＜﹣3．

∴不等式的解集为x＞ $\text{[math]}$ 或x＜﹣3．

请你仿照上述方法解决下列问题：
1. （1）求不等式（2x﹣3）（x+1）＜0的解集．
2. （2）求不等式 $\text{[math]}$ ≥0的解集．
答案解析收藏纠错 + 选题
24. (2019七下·赣县期末) 如图，在平面直角坐标系中，点A ， B的坐标分别为A（0，a），B（b ， a），且a ， b满足（a﹣3）²+|b﹣6|＝0，现同时将点A ， B分别向下平移3个单位，再向左平移2个单位，分别得到点A ， B的对应点C ， D ，连接AC ， BD ， AB ．
1. （1）求点C ， D的坐标及四边形ABDC的面积S_{四边形ABCD}；
2. （2）在y轴上是否存在一点M ，连接MC ， MD ，使S_△MCD＝ $\text{[math]}$ S_{四边形ABCD}？若存在这样一点，求出点M的坐标，若不存在，试说明理由；
3. （3）点P是直线BD上的一个动点，连接PA ， PO ，当点P在BD上移动时（不与B ， D重合），直接写出∠BAP ， ∠DOP ， ∠APO之间满足的数量关系．
答案解析收藏纠错 + 选题