

1314 1234 2333 1224 3322 1413 3124 4321 2341 2413 1224 2143 4312
2412 1413 4331 2234 4422 3241 4331 4234
 B .
B .  C .
C .  D .
D . 




(Ⅰ)求证:平面PMN⊥平面BCNM;
(Ⅱ)若点D在线段BC上,且BD=2DC,求二面角M﹣PD﹣C的余弦值.
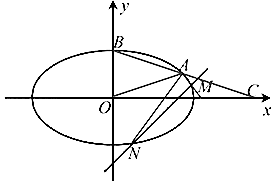
(Ⅰ)求椭圆E的标准方程;
(Ⅱ)设直线l过椭圆E的右焦点,且与椭圆E相交于M、N两点(M、N在直线 的同侧),若
,求直线l的方程.
⑴抗体检测法:每个个体独立检测,每一次检测成本为80元,每个个体收取检测费为100元.
⑵核酸检测法:先合并个体,其操作方法是:当个体不超过10个时,把所有个体合并在一起进行检测.
当个体超过10个时,每10个个体为一组进行检测.若该组检测结果为阴性(正常),则只需检测一次;若该组检测结果为阳性(不正常),则需再对每个个体按核酸检测法重新独立检测,共需检测k+1次(k为该组个体数,1≤k≤10,k∈N*).每一次检测成本为160元.假设在接受检测的个体中,每个个体的检测结果是阳性还是阴性相互独立,且每个个体是阳性结果的概率均为p(0<p<1).
(Ⅰ)现有100个个体采取抗体检测法,求其中恰有一个检测出为阳性的概率;
(Ⅱ)因大多数人群筛查出现阳性的概率很低,且政府就核酸检测法给子检测机构一定的补贴,故检测机构推出组团选择核酸检测优惠政策如下:无论是检测一次还是k+1次,每组所有个体共收费700元(少于10个个体的组收费金额不变).已知某企业现有员工107人,准备进行全员检测,拟准备9000元检测费,由于时间和设备条件的限制,采用核酸检测法合并个体的组数不得高于参加采用抗体检测法人数,请设计一个合理的的检测安排方案;
(Ⅲ)设 ,现有n(n∈N*且2≤n≤10)个个体,若出于成本考虑,仅采用一种检测方法,试问检测机构应采用哪种检测方法?(ln3≈1.099,ln4≈1.386,ln5≈1.609,ln6≈1.792)
(Ⅰ)写出曲线C的普通方程和极坐标方程;
(Ⅱ)M,N为曲线C.上两点,若OM⊥ON,求|MN|的最小值.