浙教版2019-2020学年初中数学七年级下学期期末复习专题...

更新时间：2020-07-12 浏览次数：189 类型：复习试卷

一、单选题

1. 下列各式中，不能分解因式的是（）

A . 4x²＋2xy＋ $\text{[math]}$ y² B . 4x²－2xy＋ $\text{[math]}$ y² C . 4x²－ $\text{[math]}$ y² D . －4x²－ $\text{[math]}$ y²

答案解析收藏纠错 + 选题
2. (2020七下·长兴期末) 下列各式从左到右的变形中，属于因式分解的是（）

A . (3-x)(3+x)=9-x² B . (y+1)(y-3)=-(3-y)(y+1) C . 4yz-2y²z+z=2y(2z-yz)+z D . -8x²+8x-2=-2(2x-1)²

答案解析收藏纠错 + 选题
3. (2024八上·长沙期末) 下列分解因式中，完全正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2020八下·张掖期中) 下列各组代数式中没有公因式的是（）

A . 4a²bc与8abc² B . a³b²+1与a²b³–1 C . b(a–2b)²与a（2b–a）² D . x+1与x²–1

答案解析收藏纠错 + 选题
5. (2020七上·遂宁期末) 下列添括号正确是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021八上·芙蓉月考) 若y²+my+9是一个完全平方式，则m的值为（）

A . 3 B . ±3 C . 6 D . ±6

答案解析收藏纠错 + 选题
7. (2020七下·吴兴期中) 下列多项式哪一项可以用平方差公式分解因式（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021八下·沈河期末) 下列多项式能直接用完全平方公式进行因式分解的是（）

A . x²+2x﹣1 B . x²﹣x+ $\text{[math]}$ C . x²+xy+y² D . 9+x²﹣3x

答案解析收藏纠错 + 选题
9. (2020八下·张掖期中) 下列因式分解正确的是（）

A . –4a²+4b²=–4(a²–4b²)=–4(a+2b)(a–2b) B . 3m³–12m=3m(m²–4) C . 4x⁴y–12x²y²+7=4x²y(x²–3y)+7 D . 4–9m²=(2+3m)(2–3m)

答案解析收藏纠错 + 选题
10. (2020八下·西安月考) 小强是一位密码编译爱好者，在他的密码手册中，有这样一条信息：x﹣y，a﹣b，2，x²﹣y² ， a，x+y，分别对应下列六个字：华、我、爱、美、游、中，现将2a（x²﹣y²）﹣2b（x²﹣y²）因式分解，结果呈现的密码信息可能是（）

A . 爱我中华 B . 我游中华 C . 中华美 D . 我爱美

答案解析收藏纠错 + 选题

二、填空题

11. (2020八上·张掖期末) 如果 $\text{[math]}$ 可以因式分解为 $\text{[math]}$ （其中 $\text{[math]}$ ， $\text{[math]}$ 均为整数），则 $\text{[math]}$ 的值是．

答案解析收藏纠错 + 选题
12. 多项式x²+mx+5因式分解得（x+5）（x+n），则m=，n=．

答案解析收藏纠错 + 选题
13. (2020八下·张掖期中) 将–x⁴–3x²+x提取公因式–x后，剩下的因式是.

答案解析收藏纠错 + 选题
14. (2019七下·岳阳期中) 多项式 $\text{[math]}$ 的展开结果中的 $\text{[math]}$ 的一次项系数为3，常数项为2，则 $\text{[math]}$ 的值为 .

答案解析收藏纠错 + 选题
15. (2022七下·江阴期中) 多项式 $\text{[math]}$ 加上一个单项式后，可化为一个整式的平方，则这个单项式是.（写一个即可）

答案解析收藏纠错 + 选题
16. (2024八下·中卫期末) 若 $\text{[math]}$ 可以用完全平方式来分解因式，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题

三、解答题

17. (2020八下·中宁期中) 分解因式：
1. （1） a²b－abc；
2. （2） x(m+n)-y(m+n)+(m+n)
3. （3） 9x²-16y²
4. （4） 3ax²-6axy+3ay²
答案解析收藏纠错 + 选题
18. (2019八下·太原期末) 数25⁷－5¹²能被120整除吗?请说明理由.

答案解析收藏纠错 + 选题
19. (2024七下·娄底期中) 已知二次三项式x²+px+q的常数项与（x-1）（x-9）的常数项相同，而它的一次项与（x-2）（x-4）的一次项相同，试将此多项式因式分解．

答案解析收藏纠错 + 选题
20.
1. （1）因式分解：（x-y）（3x-y）+2x（3x-y）；
2. （2）设 y=kx，是否存在实数 k，使得上式的化简结果为 x²？求出所有满足条件的 k 的值．若不能，请说明理由．
答案解析收藏纠错 + 选题
21. (2019七下·迁西期末) 解下列各题：
1. （1）分解因式：9a²（x﹣y）+4b²（y﹣x）；
2. （2）甲，乙两同学分解因式x²+mx+n，甲看错了n，分解结果为（x+2）（x+4）；乙看错了m，分解结果为（x+1）（x+9），请分析一下m，n的值及正确的分解过程．
答案解析收藏纠错 + 选题
22. (2019八上·武威月考) 下面是某同学对多项式（x²－4x+2）（x²－4x+6）+4进行因式分解的过程.
解：设x²－4x=y

原式=（y+2）（y+6）+4    （第一步）

= y²+8y+16           （第二步）

=（y+4）²            （第三步）

=（x²－4x+4）²       （第四步）

回答下列问题：
1. （1）该同学第二步到第三步运用了因式分解的_______.
  
  A . 提取公因式 B . 平方差公式 C . 两数和的完全平方公式 D . 两数差的完全平方公式
2. （2）该同学因式分解的结果是否彻底？.（填“彻底”或“不彻底”）
  若不彻底，请直接写出因式分解的最后结果.
3. （3）请你模仿以上方法尝试对多项式（x²－2x）（x²－2x+2）+1进行因式分解.
答案解析收藏纠错 + 选题
23. (2021八上·镇原期末) 阅读材料
小明遇到这样一个问题：求计算（x+2）（2x+3）（3x+4）所得多项式的一次项系数．

小明想通过计算（x+2）（2x+3）（3x+4）所得的多项式解决上面的问题，但感觉有些繁琐，他想探寻一下，是否有相对简洁的方法．

他决定从简单情况开始，先找（x+2）（2x+3）所得多项式中的一次项系数．通过观察发现：

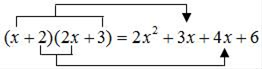
也就是说，只需用x+2中的一次项系数1乘以2x+3中的常数项3，再用x+2中的常数项2乘以2x+3中的一次项系数2，两个积相加1×3+2×2=7，即可得到一次项系数．

延续上面的方法，求计算（x+2）（2x+3）（3x+4）所得多项式的一次项系数．可以先用x+2的一次项系数1，2x+3的常数项3，3x+4的常数项4，相乘得到12；再用2x+3的一次项系数2，x+2的常数项2，3x+4的常数项4，相乘得到16；然后用3x+4的一次项系数3，x+2的常数项2，2x+3的常数项3，相乘得到18．最后将12，16，18相加，得到的一次项系数为46．

参考小明思考问题的方法，解决下列问题：
1. （1）计算（2x+1）（3x+2）所得多项式的一次项系数为．
2. （2）计算（x+1）（3x+2）（4x﹣3）所得多项式的一次项系数为．
3. （3）若计算（x²+x+1）（x²﹣3x+a）（2x﹣1）所得多项式的一次项系数为0，则a=．
4. （4）若x²﹣3x+1是x⁴+ax²+bx+2的一个因式，则2a+b的值为．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

浙教版2019-2020学年初中数学七年级下学期期末复习专题...

副标题：

*注意事项：

浙教版2019-2020学年初中数学七年级下学期期末复习专题...

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析