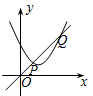
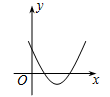
 B .
B . 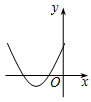 C .
C . 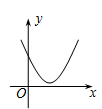 D .
D . 

|
甲社区 |
67 |
68 |
73 |
75 |
76 |
78 |
80 |
82 |
83 |
84 |
85 |
85 |
90 |
92 |
95 |
|
乙社区 |
66 |
69 |
72 |
74 |
75 |
78 |
80 |
81 |
85 |
85 |
88 |
89 |
91 |
96 |
98 |
根据以上信息解答下列问题:
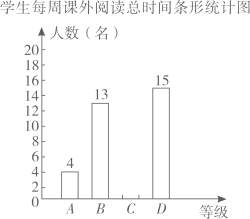
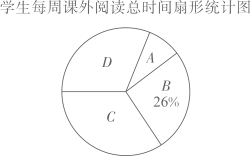
请你根据统计图的信息,解决下列问题: