(参考数据:若随机变量 服从正态分布
,则
,
,
.)
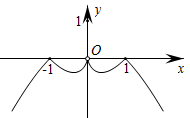
B .
B . 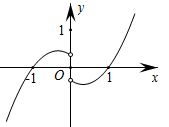
C .
C . 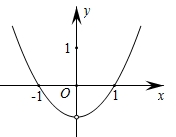
D .
D . 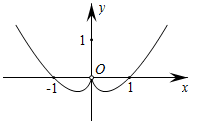

|
潜伏期 (单位:天) |
| | | | | | |
| 人数 | 85 | 205 | 310 | 250 | 130 | 15 | 5 |
附:
| | 0.05 | 0.025 | 0.010 |
| | 3.841 | 5.024 | 6.635 |
其中
.
|
潜伏期≤6天 |
潜伏期>6天 |
总计 |
|
|
50岁以上(含50岁) |
100 |
||
|
50岁以下 |
55 |
||
|
总计 |
200 |