| 男衬衫号码 | 39号 | 40号 | 41号 | 42号 | 43号 |
| 销售数量/件 | 3 | 12 | 21 | 9 | 5 |
他决定进货时,增加41号衬衫的进货数量,影响该店主决策的统计量是( )
 B .
B .  C .
C .  D .
D . 

|
所挂物体质量 | 1 | 2 | 3 | 4 | 5 |
| 弹簧长度 | 10 | 12 | 14 | 16 | 18 |
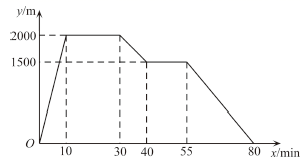
则弹簧不挂物体时的长度为 .当所挂物体质量为
时,弹簧比原来伸长了
.

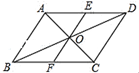
已知:四边形 是平行四边形.
求作:菱形 (点
在
上,点
在
上).
作法:①以 为圆心,
长为半径作弧,交
于点
;
②以 为圆心,
长为半径作弧,交
于点
;
③连接 .
所以四边形 为所求的菱形.
根据小明设计的尺规作图过程,

(保留作图痕迹)
证明: ,
,
.
在 中,
,
即 .
四边形
为平行四边形.()(填推理的依据)
,
四边形
为菱形.()(填推理的依据)
.七年级40名学生成绩的频数分布统计表如下.
| 成绩 | | | | | |
| 学生人数 | 3 | 12 | 13 | 11 | 1 |
.七年级成绩在
这一组的是:
70 71 71 72 73 74 74 75 76 77 78 79 79
.七、八两个年级成绩的平均分、中位数、众数和方差如下.
根据以上信息,回答下列问题:
| 年级 | 平均分 | 中位数 | 众数 | 方差 |
| 七 | 73.8 | | 88 | 127 |
| 八 | 73.8 | 75 | 84 | 99.4 |

| | | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | |
| | | 3 | 2 | 1 | 0 | 1 | | 3 | 4 | |
①求m的值;
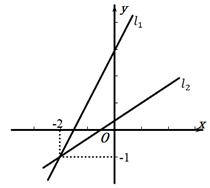
②如图,在平面直角坐标系 中,描出补全后的表中各组对应值所对应的点,并画出该函数的图象;

①求点 的坐标;
②直接写出区域 内的整点个数;

经过思考,小聪展示了一种正确的解题思路.取 的中点
,连接
,则
为等腰直角三角形,这时只需证
与
全等即可.在此基础上,同学们进行了进一步的探究:
