 B .
B . 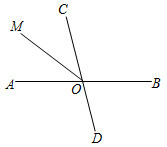
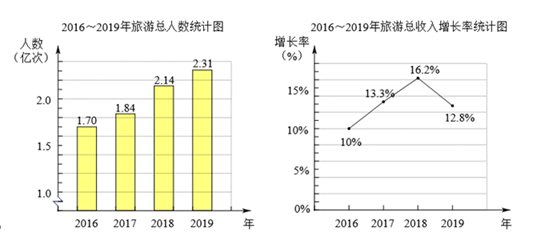
下面有三个推断:
① 从 2016 年到 2019 年,年旅游总人数增长最多的是 2018 年,比上一年增长了 0.3 亿人次;
② 从 2016 年到 2019 年,年旅游总收入最高的是 2018 年;
③ 如果 2016 年旅游总收入为 2 442.1 亿元,那么 2015 年旅游总收入约为 2 220 亿元. 其中所有合理的推断的序号是( )
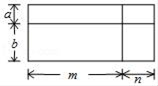

解不等式 ,并把它的解集在数轴上表示出来.
以下是小明的解答过程:
解:第一步 去分母,得15 - 3x≥2(7 - x) ,
第二步 去括号,得15 - 3x≥14 - 2x ,
第三步 移项,得
-3x + 2x≥14 - 15 ,
第四步 合并同类项,得-x≥ - 1 ,
第五步 系数化为 1,得x≥1.
第六步 把它的解集在数轴上表示为:
老师看后说:“小明的解题过程有不符合题意!”
问:请指出小明从第几步开始出现了不符合题意,并说明判断依据.
答:.
[(2x - y )2 + x ( y - 4x) + 8 y2 ]÷3y , 其中 x = 3 , y = -1
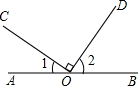
求证:∠1+∠3 = 180°

证明:∵ AB∥CD(已知),
∴ ∠1+∠2 = 180°()
又∵ ∠2 = ∠3()
∴ ∠1+∠3=180°()
求证:∠2 = ∠C .
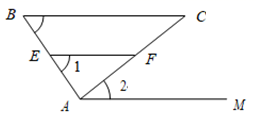
证明:∵ ∠1 = ∠B(已知),
∴ EF∥BC()
∵ AM∥EF(已知),
∴ AM∥BC()
∴ ∠2 = ∠C()


A.对七年级(1)班的全体同学进行问卷调查
B.对七年级各班的班长进行问卷调查
C.对七年级各班学号为 3 的倍数的全体同学进行问卷调查
① 在扇形统计图中“10次以下”所在的扇形的圆心角等于度;
② 补全条形统计图;
③ 根据调查结果,估计七年级每月使用公共自行车次数是“16 至 20 次”的同学有人.
提示1:用“不完全归纳法”推导{x} 与 x , x + 1的大小关系;
提示2:用“代数推理”的方法推导{x} 与 x , x + 1的大小关系.
①直接写出满足{3m + 7} = 4 的 m 取值范围;
②直接写出方程{3.5n - 2} = 2n + 1 的解..