福建省三明市梅列区2019-2020学年八年级上学期数学期中...

更新时间：2020-11-06 浏览次数：130 类型：期中考试

一、单选题

1. (2019八上·梅列期中) 在-3.14， $\text{[math]}$ ， $\text{[math]}$ ，3.121121112这些实数.无理数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 3.121121112 D . 3.14

答案解析收藏纠错 + 选题
2. (2021八下·曹县期中) $\text{[math]}$ 的平方根是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 2 D . ±2

答案解析收藏纠错 + 选题
3. (2021八上·盐都期末) 如图，小手盖住的点的坐标可能为（）

A . (3，2) B . (-3，2) C . (-3，-2) D . (3，-2)

答案解析收藏纠错 + 选题
4. (2019八上·梅列期中) 下列各点在一次函数y=2x-1图象上的是（）

A . （0，1） B . （2，-1） C . （1，1） D . （-1，1）

答案解析收藏纠错 + 选题
5. (2024七下·滨海期中) 估计 $\text{[math]}$ 的值在（）

A . 1和2之间 B . 2和3之间 C . 3和4之间 D . 4和5之间

答案解析收藏纠错 + 选题
6. (2023八下·蚌埠月考) 下列各式计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2019八上·梅列期中) 如图，点E在正方形ABCD内，满足∠AEB=90°，AE=3，BE=4，则阴影部分的面积是（）

A . 12 B . 15 C . 19 D . 20

答案解析收藏纠错 + 选题
8. (2019八上·梅列期中) 下列根式.是最简二次根式的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ （n是正整数）

答案解析收藏纠错 + 选题
9. (2019八上·梅列期中) 在平面直角坐标系.若直线y=kx+b经过第一、三、四象限，则直线y=bx-k不经过的象限是（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
10. (2019八上·梅列期中) 巫溪某中学组织初一初二学生举行“四城同创”宣传活动，从学校坐车出发，先上坡到达A地后，宣传8分钟；然后下坡到B地宣传8分钟返回，行程情况如图．若返回时，上、下坡速度仍保持不变，在A地仍要宣传8分钟，那么他们从B地返回学校用的时间是（）

A . 45.2分钟 B . 48分钟 C . 46分钟 D . 33分钟

答案解析收藏纠错 + 选题

二、填空题

11. (2024七下·武昌月考) 计算： $\text{[math]}$ =．

答案解析收藏纠错 + 选题
12. (2021八下·增城期末) 如图由于台风的影响，一棵树在离地面 $\text{[math]}$ 处折断，树顶落在离树干底部 $\text{[math]}$ 处，则这棵树在折断前的高度是.

答案解析收藏纠错 + 选题
13. (2019八上·梅列期中) 比较大小 $\text{[math]}$ 0.5．

答案解析收藏纠错 + 选题
14. (2019八上·梅列期中) 若点M(﹣3，b)与点N(a，2)关于x轴对称，则a+b=.

答案解析收藏纠错 + 选题
15. (2019八上·梅列期中) 为节约用水,某市居民生活用水按级收费,具体收费标准如下表：

用水量（吨）

不超过15吨的部分

超过15不超过25吨的部分

超过25吨的部分

单位（元/吨）

3

5

7

设李红家某月的为x吨(15<x⩽25)，应付水费为y元，则y关于x的函数表达式为．

答案解析收藏纠错 + 选题
16. (2019八上·梅列期中) 如图，Rt△ABC纸片.∠C=90°，AC=BC=4，点D在边BC上，以AD为折痕，将△ABD折叠，得到△AB′D，AB′与边BC交于点E．若△DEB′为直角三角形，则BD的长是．

答案解析收藏纠错 + 选题

三、解答题

17. (2019八上·梅列期中)
1. （1） $\text{[math]}$ ．
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
18. (2019八上·梅列期中) 先化简再求值：(x−2y)(x+2y)−4y(x−y)，其中 $\text{[math]}$ ， $\text{[math]}$ ．

答案解析收藏纠错 + 选题
19. (2019八上·梅列期中) 如图在平面直角坐标系.△ABC各顶点的坐标分别为：A(4，0)，B(−1，4)，C(−3，1)．
1. （1）在图中作△A′B′C′，使△A′B′C′和△ABC关于x轴对称；
2. （2）写出点B′的坐标；
3. （3） △A′B′C′的面积为平方单位．
答案解析收藏纠错 + 选题
20. (2019八上·梅列期中) 如图所示，圆柱的底面周长为24cm，AC是底面圆的直径，高BC＝7.5cm，点P是母线BC一点，且 $\text{[math]}$ ．一只蚂蚁从A点出发，沿着圆柱体的表面爬行到点P的最短距离是多少？（请画图解答）

答案解析收藏纠错 + 选题
21. (2019八上·梅列期中) 已知，M= $\text{[math]}$ 是9的算术平方根，N= $\text{[math]}$ 是n+10的立方根，求 $\text{[math]}$ 的值．

答案解析收藏纠错 + 选题
22. (2019八上·梅列期中) 已知一次函数y=（2m-3）x+m+1经过点A（1，4）
1. （1）求m的值；
2. （2）画出此一次函数的图象；
3. （3）若一次函数交y轴于点B，求△OAB的面积．
答案解析收藏纠错 + 选题
23. (2023八上·东阳月考) 在一条东西走向河的一侧有一村庄C，河边原有两个取水点A，B，其中AB＝AC，由于某种原因，由C到A的路现在已经不通，某村为方便村民取水决定在河边新建一个取水点H（A、H、B在一条直线上），并新修一条路CH，测得CB＝3千米，CH＝2.4千米，HB＝1.8千米．
1. （1）问CH是否为从村庄C到河边的最近路？（即问：CH与AB是否垂直？）请通过计算加以说明；
2. （2）求原来的路线AC的长．
答案解析收藏纠错 + 选题
24. (2019八上·梅列期中) 认真阅读下列材料，然后完成解答：
（材料）

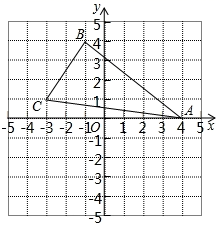
如图，已知平面直角坐标系中两点A（x₁ ， y₁）、B（x₂ ， y₂），如何求A、B两点间的的距离|AB|的值？

过点A向y轴作垂线AN₁、过点B向x轴作垂线BM₂ ，垂足分别为N₁（0，y₁）和M₂（x₂ ， 0），直线AN₁和BM₂相交于点Q．

在Rt△AQB.|AB|²= |AQ|²+ |BQ|²

为了计算AQ和BQ，过点A向x轴作垂线，垂足为M₁（x₁ ， 0）；过点B向y轴作垂线，垂足为N₂（0，y₂），于是有|AQ|=|M₁M₂|=|x₃-x₁|，|BQ|=|N₁N₂|=|y₂-y₁|．

所以，|AB|²= $\text{[math]}$ ．

由此得到A（x₁ ， y₁）、B（x₂ ， y₂）两点间的距离公式： $\text{[math]}$ ．

根据定义：两点之间线段的长度，叫做这两点之间的距离．

因此，线段AB的长度计算公式为 $\text{[math]}$ ．
1. （1）（问题）
  平面直角坐标系中有两点A（0，1）、B（2，3），求线段AB的长；
2. （2） $\text{[math]}$ 表示线段MN的长，其中点M的坐标为（a，b），点N的坐标为；
3. （3）如图，在x轴上有一点P（x，0），试求PA+PB的最小值．
答案解析收藏纠错 + 选题
25. (2019八上·梅列期中) Rt△ABC.∠C=90°，AC=6，BC=8，D是AB的中点，E、F分别是AC、BC上两点，且ED⊥FD．
1. （1）如图1，若E是AC中点，则BF=，EF=，AE²+BF²EF²（填“>，<或=”）；
2. （2）如图2，若点E是AC边上任意一点，AE²+BF²EF²（填“>，<或=”），请说明理由；
3. （3）若点E在CA延长上，（2）中三条线段之间的关系是否成立？请画图说明．
答案解析收藏纠错 + 选题