河南省南阳市唐河县2019-2020学年七年级上学期数学期中...

更新时间：2024-07-13 浏览次数：248 类型：期中考试

一、选择题

1. (2024七上·石柱月考) 中国人很早开始使用负数，中国古代数学著作《九章算术》的“方程”一章，在世界数学史上首次正式引入负数．如果收入100元记作+100元．那么﹣80元表示（）

A . 支出20元 B . 收入20元 C . 支出80元 D . 收入80元

答案解析收藏纠错 + 选题
2. (2019七上·唐河期中) 2019 年政府工作报告指出，我国经济运行保持在合理区间，国内生产总值增长6.6%，总量突破90万亿元。90万亿用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2019七上·卫辉期中) 下列算式中，运算结果为负数的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2019七上·唐河期中) 如图为某地十月份某一天的天气预报，该地这一天最高气温比最低气温高（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2019七上·唐河期中) 已知a＜b，那么a-b和它的相反数的差的绝对值是（）

A . b-a B . 2b-2a C . -2a D . 2b

答案解析收藏纠错 + 选题
6. (2023七上·龙江期中) 下列由四舍五入得到的近似数说法正确的是（）

A . 0.520精确到百分位 B . 3.056×10⁴精确到千分位 C . 6.3万精确到十分位 D . 1.50精确到0.01

答案解析收藏纠错 + 选题
7. (2019七上·唐河期中) 若 $\text{[math]}$ 是最大的负整数， $\text{[math]}$ 是绝对值最小的有理数， $\text{[math]}$ 是倒数等于它本身的自然数，则代数式 $\text{[math]}$ 的值为（）

A . 0 B . 2 C . 2019 D . 2020

答案解析收藏纠错 + 选题
8. (2024七上·武平期末) 下列说法错误的是（）

A . $\text{[math]}$ 是二次三项式 B . $\text{[math]}$ 不是单项式 C . $\text{[math]}$ 的系数是 $\text{[math]}$ D . $\text{[math]}$ 的次数是6

答案解析收藏纠错 + 选题
9. (2019七上·卫辉期中) 已知a、b、c三个数在数轴上对应点的位置如图所示，下列几个判断：①a<c<b；②-a<b；③a+b>0；④c-a<0中，错误的个数是（）个.

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
10. (2019七上·唐河期中) 下列语句中正确的个数是（）
① $\text{[math]}$ 是最小的整数:② $\text{[math]}$ 是最大的负有理数:③在数轴上到原点的距离为 $\text{[math]}$ 的点表示的数是 $\text{[math]}$ ;④有绝对值最小的有理数;⑤绝对值是本身的数是正数;⑥有理数的绝对值都是正数

A . 0个 B . 1个 C . 2个 D . 3个

答案解析收藏纠错 + 选题

二、填空题

11. (2019七上·唐河期中) 比较大小: $\text{[math]}$ $\text{[math]}$ (填“ $\text{[math]}$ ”，“ $\text{[math]}$ "或“ $\text{[math]}$ ”)

答案解析收藏纠错 + 选题
12. (2019七上·唐河期中) 果商品的原价是每件 $\text{[math]}$ 元，在销售时每件加价 $\text{[math]}$ 元，再降价 $\text{[math]}$ ，则现在每件的售价是元.

答案解析收藏纠错 + 选题
13. (2019七上·唐河期中) 代数式 $\text{[math]}$ 按 $\text{[math]}$ 的升幂排列正确的是.

答案解析收藏纠错 + 选题
14. (2020七上·永年月考) 如图，是一个简单的数值计算程序，当输入的x的值为5，则输出的结果为.

答案解析收藏纠错 + 选题
15. (2019七上·唐河期中) 如图，用黑白两种颜色的正六边形地面砖按如下所示的规律，拼成若干个图案，第 $\text{[math]}$ 个图案中有白色的地面砖块.

答案解析收藏纠错 + 选题

三、解答题

16. (2019七上·唐河期中) 计算
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
3. （3） $\text{[math]}$
答案解析收藏纠错 + 选题
17. (2020七上·新乡期中) 把下列六个数： $\text{[math]}$
1. （1）分别在数轴上表示出来，并用“ $\text{[math]}$ ”把它们按从小到大的顺序连结起来：
2. （2）填入相应的大括号内
  整数集{ ……}
  
  负分数集{ ……}
答案解析收藏纠错 + 选题
18. (2021七上·黑山期中) 新学期开学，两摞规格相同准备发放的数学课本整齐地叠放在讲台上，请根据图中所给的数据信息，解答下列问题：
1. （1）一本数学课本的高度是多少厘米？
2. （2）讲台的高度是多少厘米？
3. （3）请写出整齐叠放在桌面上的x本数学课本距离地面的高度的代数式(用含有x的代数式表示)；
4. （4）若桌面上有56本同样的数学课本，整齐叠放成一摞，从中取走18本后，求余下的数学课本距离地面的高度.
答案解析收藏纠错 + 选题
19. (2019七上·唐河期中) 学习有理数的乘法后，老师给同学们这样一道题目：计算：49 $\text{[math]}$ ×（-5），看谁算的又快又对，有两位同学的解法如下：
聪聪；原式=- $\text{[math]}$ ×5=- $\text{[math]}$ -249 $\text{[math]}$ ；

明明：原式=（49+ $\text{[math]}$ ）×（-5）=49×（-5）+ $\text{[math]}$ ×（-5）=-249 $\text{[math]}$ ，
1. （1）对于以上两种解法，你认为谁的解法较好？
2. （2）上面的解法对你有何启发，你认为还有更好的方法吗？如果有，请把它写出来；
3. （3）用你认为最合适的方法计算：39 $\text{[math]}$ ×（-8）.
答案解析收藏纠错 + 选题
20. (2019七上·唐河期中) 甲、乙两家商场以同样的价格出售同样的电器，但各自推出的优惠方案不同.甲商场规定：凡超过1000元的电器，超出的金额按90%收取;乙商场规定：凡超过500元的电器，超出的金额按95%收取. 某顾客购买的电器价格是x元.
1. （1）当x=850时，该顾客应选择在商场购买比较合算;
2. （2）当x>1000时，分别用代数式表示在两家商场购买电器所需付的费用;
3. （3）当x=1700时，该顾客应选择哪一家商场购买比较合算?说明理由.
答案解析收藏纠错 + 选题
21. (2020七上·乐山期中) 已知代数式 $\text{[math]}$ ，当 $\text{[math]}$ 时，该代数式的值为3.
1. （1）求c的值；
2. （2）已知：当 $\text{[math]}$ 时，该代数式的值为0.
  ①求：当 $\text{[math]}$ 时，该代数式的值；
  
  ②若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，试比较a与d的大小，并说明理由.
答案解析收藏纠错 + 选题
22. (2021七上·岐山期中) 某出租车驾驶员从公司出发，在东西向的路上连续接送5批客人，行驶路程记录分别为：+5，+2，﹣4，﹣3，+10（规定向东为正，向西为负，单位：千米）
1. （1）接送完第5批客人后，该驾驶员在公司的什么方向？距离公司多少千米？
2. （2）若该出租车每千米耗油0.2升，则在这个过程中共耗油多少升？
3. （3）若该出租车的计价标准为行驶路程不超过3千米收费10元，超过3千米的部分按每千米1.8元收费，在这过程该驾驶员共收到车费多少？
答案解析收藏纠错 + 选题
23. (2019七上·唐河期中) 问题：如何快速计算1+2+3+…+n 的值呢？
1. （1）探究：令s=1+2+3+…+n①，则s=n+n-1+…+2+1②
  ①+②得2s=(n+1)(n+1)+…+(n+1)=n $\text{[math]}$ (n+1)
  
  因此 $\text{[math]}$ .
2. （2）应用：
  ①计算： $\text{[math]}$ ；
  
  ②如图1，一串连续的整数1，2，3，4，…，自上往下排列，最上面一行有一个数，以下各行均比上一行多一个数字，若共有15行数字，则最底下一行最左边的数是；
  
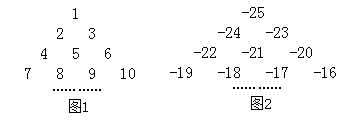
  ③如图2，一串连续的整数-25，-24，-23，…，按图1方式排列，共有14行数字，求图2中所有数字的和.
答案解析收藏纠错 + 选题