



|
x |
… |
… |
|||||
|
y |
… |
… |

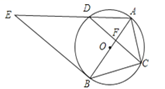
①分别求出当0≤t≤50和50<t≤100时,y与t的函数关系式;
②设将这批小龙虾放养t天后一次性出售所得利润为W元,求当t为何值时,W最大?并求出最大值.(利润=销售总额﹣总成本)

因为 ,所以把
绕点
逆时针旋转90°至
,可使
与
重合.因为
,所以
,点
共线.
根据,易证 ,得
.请证明.
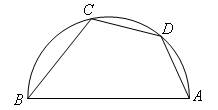
如图②,四边形 中,
,
,点
分别在边
上,
.若
都不是直角,则当
与
满足等量关系时,
仍然成立,请证明.

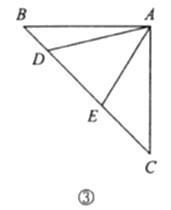
如图③,在 中,
,点
均在边
上,且
.猜想
应满足的等量关系,并写出证明过程.


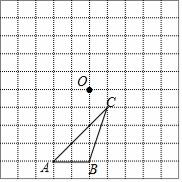
②是否存在点D,使CE与DF互相垂直平分?若存在,请求出点D的坐标;若不存在,请说明理由.