初中数学苏科版八年级上册 6.4用一次函数解决问题同步练习

更新时间：2020-10-27 浏览次数：255 类型：同步测试

一、单选题

1. 鲁老师乘车从学校到省城去参加会议，学校距省城200千米，车行驶的平均速度为80千米/时．x小时后鲁老师距省城y千米，则y与x之间的函数关系式为（）

A . y=80x-200 B . y=-80x-200 C . y=80x+200 D . y=-80x+200

答案解析收藏纠错 + 选题
2. (2019八下·平潭期末) 等腰三角形的周长为20，设底边长为x，腰长为y，则y关于x的函数解析式为（x为自变量）（　　）

A . y＝20﹣x B . y＝20﹣2x C . y＝10﹣ $\text{[math]}$ x D . y＝20﹣ $\text{[math]}$ x

答案解析收藏纠错 + 选题
3. (2024八下·卢龙期中) 向最大容量为60升的热水器内注水，每分钟注水10升，注水2分钟后停止1分钟，然后继续注水，直至注满.则能反映注水量与注水时间函数关系的图象是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2019八下·双鸭山期末) 小亮从家步行到公交车站台，等公交车去学校. 图中的折线表示小亮的行程s(km)与所花时间t(min)之间的函数关系. 下列说法不正确的是（）

A . 他离家8km共用了30min B . 他等公交车时间为6min C . 他步行的速度是100m/min D . 公交车的速度是350m/min

答案解析收藏纠错 + 选题
5. (2019八上·包河期中) 广宇同学以每千克1.1元的价格从批发市场购进若干千克西瓜到周谷堆市场上销售，在销售了40千克之后，余下的打七五折全部售完．销售金额y（元）与售出西瓜的千克数x（千克）之间的关系如图所示．下列结论正确的是（）

A . 降价后西瓜的单价为2元/千克 B . 广宇一共进了50千克西瓜 C . 售完西瓜后广宇获得的总利润为44元 D . 降价前的单价比降价后的单价多0.6元

答案解析收藏纠错 + 选题
6. (2020八下·广州期中) 在一条笔直的公路上有A、B两地，甲乙两人同时出发，甲骑自行车从A地到B地，乙骑自行车从B地到A地，到达A地后立即按原路返回B地.如图是甲、乙两人离B地的距离 $\text{[math]}$ 与行驶时间 $\text{[math]}$ 之间的函数图象，下列说法中①A、B两地相距30千米；②甲的速度为15千米/时；③点M的坐标为( $\text{[math]}$ ，20)；④当甲、乙两人相距10千米时，他们的行驶时间是 $\text{[math]}$ 小时或 $\text{[math]}$ 小时. 正确的个数为（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
7. 一辆汽车和一辆摩托车分别从A，B两地去同一个城市，它们离A地的路程随时间变化的图象如图所示．则下列结论：
①摩托车比汽车晚到lh；②A、B两地的路程为20km；③摩托车的速度为45km/h，汽车的速度为60km/h；④汽车出发1h后与摩托车相遇，此时距B地40km．其中正确结论的个数是（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
8. (2019八下·闽侯期中) 甲乙两人匀速从同一地点到1500米处的图书馆看书，甲出发5分钟后，乙以50米/分的速度沿同一路线行走．设甲乙两人相距s（米），甲行走的时间为t（分），s关于t的函数图象的一部分如图所示．下列结论正确的个数是（）
（1）t＝5时，s＝150；（2）t＝35时，s＝450；（3）甲的速度是30米/分；（4）t＝12.5时，s＝0．

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
9. (2021八上·连云月考) “龟兔首次赛跑”之后，输了比赛的兔子总结惨痛教训后.决定和乌龟再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事（ $\text{[math]}$ 表示乌龟从起点出发所行的时间， $\text{[math]}$ 表示乌龟所行的路程， $\text{[math]}$ 表示兔子所行的路程.下列说法中：①“龟兔再次赛跑”的路程为1000米；②兔子和乌龟同时从起点出发；③乌龟在途中休息了10分钟；④兔子在途中750米处上了乌龟.正确的有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
10. (2022八上·西安月考)
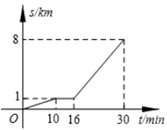
甲、乙两车从A地驶向B地，并以各自的速度匀速行驶，甲车比乙车早行驶2h，并且甲车途中休息了0.5h（甲车休息前后的速度相同），甲、乙两车行驶的路程y（km）与行驶的时间x（h）的函数图象如图所示．根据图象的信息有如下四个说法：
①甲车行驶40千米开始休息
②乙车行驶3.5小时与甲车相遇
③甲车比乙车晚2.5小时到到B地
④两车相距50km时乙车行驶了 $\text{[math]}$ 小时
其中正确的说法有（　　）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题

11. (2023·清新模拟) 小华向果农买西红柿，连同竹篮称得总质量为3千克，需付西红柿的钱10元，若再加买0.5千克的西红柿，需多付2元，则空竹篮的质量为千克。

答案解析收藏纠错 + 选题
12. (2021七下·甘州期中) 汽车以60千米/时的平均速度，由A地驶往相距420千米的上海，汽车距上海的路程s（千米）与行驶时间t（时）的函数关系式是．

答案解析收藏纠错 + 选题
13. (2021八上·沈河期末) 一个弹簧不挂重物时长10cm，挂上重物后伸长的长度与所挂重物的质量成正比，如果挂上1kg的物体后，弹簧伸长3cm，则弹簧总长y(单位：cm)关于所挂重物x(单位：kg)的函数关系式为(不需要写出自变量取值范围)

答案解析收藏纠错 + 选题
14. (2024八上·富川期末) 李老师开车从甲地到相距 $\text{[math]}$ 千米的乙地，如果油箱剩余油量 $\text{[math]}$ （升）与行驶里程 $\text{[math]}$ （千米）之间是一次函数关系，其图像如图所示，那么到达乙地时油箱剩余油量是升．

答案解析收藏纠错 + 选题
15. (2019八下·大名期末) 如图，折线ABC是某市在2018年乘出租车所付车费y（元）与行车里程x（km）之间的函数关系图像，观察图像回答，乘客在乘车里程超过3千米时，每多行驶1km，要再付费元．

答案解析收藏纠错 + 选题
16. (2022八上·薛城期中) 如图所示，甲、乙两车在某时间段内速度随时间变化的图象．下列结论：
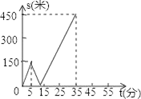
①甲的速度始终保持不变；

②乙车第12秒时的速度为32米/秒；

③乙车前4秒行驶的总路程为48米.

其中正确的是．（填序号）

答案解析收藏纠错 + 选题
17. (2023·长清模拟) AB两地相距20km，甲从A地出发向B地前进，乙从B地出发向A地前进，两人沿同一直线同时出发，甲先以8km/h的速度前进1小时，然后减慢速度继续匀速前进，甲乙两人离A地的距离S（km）与时间t（h）的关系如图所示，则甲出发小时后与乙相遇．

答案解析收藏纠错 + 选题
18. (2018八上·银川期中) 甲、乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发向乙地.如图，线段OA表示货车离甲地距离y（千米）与时间x（小时）之间的函数关系式；折线B﹣C﹣D表示轿车离甲地距离y（千米）与x（小时）之间的函数关系.
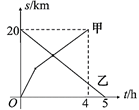
下面几种说法：①货车的速度为60千米/小时；

②轿车与货车相遇时，货车恰好从甲地出发了3小时；

③若轿车到达乙地后，马上沿原路以CD段速度返回，则轿车从乙地出发 $\text{[math]}$ 小时再次与货车相遇；其中正确的是.（填写序号）

答案解析收藏纠错 + 选题
19. (2020八下·河北期中) 如图所示的图像反映的过程是：甲乙两人同时从 $\text{[math]}$ 地出发，以各自的速度匀速向 $\text{[math]}$ 地行驶，甲先到 $\text{[math]}$ 地停留半小时后，按原路以另一速度匀速返回，直至与乙相遇.乙的速度为 $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$ 表示甲乙两人相距的距离， $\text{[math]}$ $\text{[math]}$ 表示乙行驶的时间.现有以下 $\text{[math]}$ 个结论：① $\text{[math]}$ 、 $\text{[math]}$ 两地相距 $\text{[math]}$ ；②点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ；③甲去时的速度为 $\text{[math]}$ ；④甲返回的速度是 $\text{[math]}$ .以上 $\text{[math]}$ 个结论中正确的是.

答案解析收藏纠错 + 选题
20. (2020八上·包河期末) 如图是本地区一种产品30天的销售图象，图1是产品日销售量y（单位：件）与时间t（单位：天）的函数关系，图2是一件产品的销售利润z（单位，元）与时间t（单位：天）的函数关系，已知日销售利润=日销售量×一件产品的销售利润，下列正确结论的序号是．

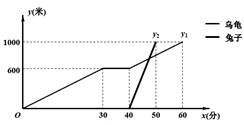
①第24天的销售量为200件；

②第10天销售一件产品的利润是15元；

③第12天与第30天这两天的日销售利润相等；

④第30天的日销售利润是750元．

答案解析收藏纠错 + 选题

三、解答题

21. (2020八下·黄石期中) 甲、乙两家旅行社为了吸引更多的顾客，分别提出了赴某地旅游的团体优惠方法，甲旅行社的优惠方法是：买4张全票，其余人按半价优惠；乙旅行社的优惠方法是：一律按7折优惠，已知两家旅行社的原价均为每人100元；那么随着团体人数的变化，哪家旅行社的收费更优惠？

答案解析收藏纠错 + 选题
22. (2020八下·通州月考) 如图，在靠墙（墙长为18m）的地方围建一个矩形的养鸡场，另三边用竹篱笆围成，如果竹篱笆总长为35m，求鸡场的长y （m）与宽x （m）的函数关系式，并求自变量的取值范围.

答案解析收藏纠错 + 选题
23. 甲、乙两车从A地驶向B地，并以各自的速度匀速行驶，甲车比乙车早行驶2h，并且甲车途中休息了0.5h，如图是甲乙两车行驶的距离y（km）与时间x（h）的函数图象．
1. （1）求出图中m，a的值；
2. （2）求出甲车行驶路程y（km）与时间x（h）的函数解析式，并写出相应的x的取值范围；
3. （3）当乙车行驶多长时间时，两车恰好相距50km．
答案解析收藏纠错 + 选题
24. 某天早晨，张强从家跑步去体育锻炼，同时妈妈从体育场晨练结束回家，途中两人相遇，张强跑到体育场后发现要下雨，立即按原路返回，遇到妈妈后两人一起回到家（张强和妈妈始终在同一条笔直的公路上行走）．如图是两人离家的距离y（米）与张强出发的时间x（分）之间的函数图象，根据图象信息解答下列问题：
1. （1）求张强返回时的速度；
2. （2）妈妈比按原速返回提前多少分钟到家？
3. （3）请直接写出张强与妈妈何时相距1200米？
答案解析收藏纠错 + 选题
25. (2019八上·兴化月考) 一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为x(h)，两车之间的距离为y(km)，图中的折线表示y与x之间的函数关系.
根据图象进行以下探究：
1. （1）请问甲乙两地的路程为；
2. （2）求慢车和快车的速度；
3. （3）求线段BC所表示的y与x之间的函数关系式，并写出自变量x的取值范围；
4. （4）如果设慢车行驶的时间为x(h)，快慢两车到乙地的距离分别为y₁(km)、y₂(km)，请在右图中画出y₁、y₂与x的函数图象.
答案解析收藏纠错 + 选题
26. (2018八上·双城期末) 如图，在平面直角坐标系中，点A坐标为(6，0)，点B在y轴的正半轴上，且 $\text{[math]}$ =24 ，
1. （1）求点B坐标；
2. （2）若点P从B出发沿y轴负半轴方向运动，速度每秒2个单位，运动时间t秒，△AOP的面积为S，求S与t的关系式，并直接写出t的取值范围；
3. （3）在(2)的条件下，若S△AOP：S△ABP=1：3，且S△AOP+S△ABP=S△AOB，在线段AB的垂直平分线上是否存在点Q，使得△AOQ的面积与△BPQ的面积相等？若存在，求出Q点坐标；若不存在，请说明理由。
答案解析收藏纠错 + 选题
27. (2021八上·崇左期末) 某公司计划购买若干台电脑，现从两家商场了解到同一种型号的电脑报价均为 $\text{[math]}$ 元，并且多买都有一定的优惠. 各商场的优惠条件如下：
甲商场优惠条件：第一台按原价收费，其余的每台优惠 $\text{[math]}$ ；

乙商场优惠条件：每台优惠 $\text{[math]}$ .
1. （1）设公司购买 $\text{[math]}$ 台电脑，选择甲商场时，所需费用为 $\text{[math]}$ 元，选择乙商场时，所需费用为 $\text{[math]}$ 元，请分别求出 $\text{[math]}$ 与 $\text{[math]}$ 之间的关系式.
2. （2）什么情况下，两家商场的收费相同？什么情况下，到甲商场购买更优惠？什么情况下，到乙商场购买更优惠？
3. （3）现在因为急需，计划从甲乙两商场一共买入 $\text{[math]}$ 台某品牌的电脑，其中从甲商场购买 $\text{[math]}$ 台电脑.已知甲商场的运费为每台 $\text{[math]}$ 元，乙商场的运费为每台 $\text{[math]}$ 元，设总运费为 $\text{[math]}$ 元，在甲商场的电脑库存只有 $\text{[math]}$ 台的情况下，怎样购买，总运费最少？最少运费是多少？
答案解析收藏纠错 + 选题